Area tra due curve

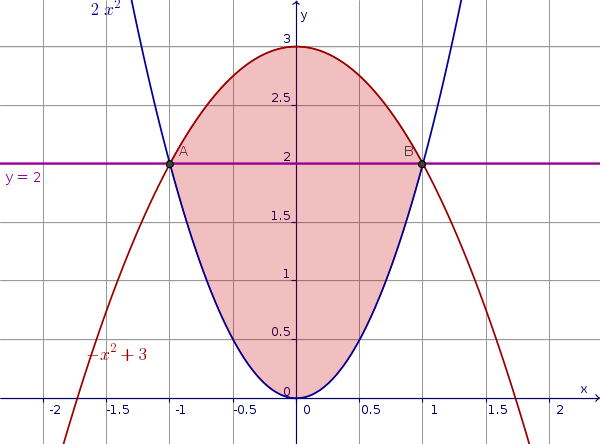
Calcolare l'area compresa tra le seguenti funzioni:

$$ \begin{cases} y = 2 x^2 \\ y = 3 - x^2 \end{cases} $$

Si tratta di due parabole. La prima ha vertice nell'origine, e concavità verso l'alto; la seconda ha vertice in (0;3), e concavità verso il basso.

Per trovare i punti comuni tra le due curve si deve risolvere il sistema; eliminando la y si ha subito un'equazione di secondo grado:

$ \begin{array} \\2x^2 = 3 - x^2 \\3x^2 - 3 = 0 \end{array} $

Questa equazione si può risolvere anche senza la classica formuletta, p.es. scomponendo il polinomio a primo membro:

$ 3x^2 - 3 = 3(x^2 - 1) = 3(x - 1)(x + 1) $

Dunque l'equazione ha due soluzioni, $x = -1 ; x = 1$ corrispondenti ai punti comuni A(1;2) e B(-1;2) come è evidente anche dal disegno.

Per calcolare l'area della regione di piano delimitata dalle due curve occorre calcolare l'integrale definito tra -1 e 1 della differenza tra la parabola superiore ($ y = 3 - x^2 $) e quella inferiore ($ y = 2 x^2 $):

$ \int^{1}_{-1}(3 - x^2 - 2x^2)dx = \int^{1}_{-1}(3 - 3x^2)dx = \\ [3x - x^3]^1_{-1} = (3 - 1) - (-3 + 1) = 2 + 2 = 4 $

L'area tra le due curve vale quindi 4. Osservando il disegno si contano 8 quadratini (che equivalgono a $ \frac{1}{4} $) completamente inclusi, 10 in maggioranza inclusi e 4 frammenti in buon accordo con il risultato trovato.

Una verifica esatta si può fare usando il teorema di Archimede (l'area del segmento parabolico è i quattro terzi di quella del triangolo inscritto) ai due segmenti parabolici sopra e sotto la retta $y = 2$:

1. Il triangolo superiore ha base 2 e altezza 1, quindi area = 1; il segmento parabolico ha area $ \frac{4}{3} $
2. Il triangolo superiore ha base 2 e altezza 2, quindi area = 2; il segmento parabolico ha area $ \frac{8}{3} $

quindi in totale: $ \frac{4}{3} + \frac{8}{3} = \frac{12}{3} = 4$

Esercizi

1. Calcolare l'area compresa tra le parabole $f(x)=-{x^2} +x +4$ e $g(x)={x^2} +x -4$ .(*)
2. Calcolare l'area compresa tra le parabole $f(x)=\frac{x^2}{4} -x -1$ e $g(x)=-x^2 + \frac{3}{2} x + 9$ .(*)
3. Calcolare l'area compresa tra le parabole $f(x)=-\frac{x^2}{2} +x +2$ e $g(x)=-{x^2}+x+4$ .(*)