

|
Calcolare l'area compresa tra le seguenti funzioni:
$$ \begin{array} \\y = x^3 - x^2 \\y = x - 1 \end{array} $$
Si tratta di una cubica e di una retta. La cubica può scriversi anche come
$ y = x^2(x - 1) $
e quindi ha due zeri, uno doppio (tangente all'asse delle x) $x = 0$ e uno semplice $x = +1$;
Per trovare i punti comuni tra le due curve si deve risolvere il sistema; eliminando la y si ha subito un'equazione algebrica di terzo grado:
$ x^3 - x^2 = x - 1 \\ x^3 - x^2 - x + 1 = 0 $
Questa equazione si può risolvere in diversi modi; p.es. scomponendo a fattor parziale il polinomio a primo membro:
$ x^2(x - 1) - (x - 1) = (x - 1)(x^2 - 1) = (x - 1)(x - 1)(x + 1) = (x - 1)^2(x + 1) $
Altra possibilità: avendo riconosciuto che il polinomio si annulla per x = 1, dividerlo, in base al teorema di Ruffini, per (x - 1) ottenendo un polinomio (e quindi un'equazione) di secondo grado.
Dunque l'equazione ha due soluzioni, una semplice x = -1 e una doppia x = 1. Questo vuole dire che per x = 1 le due curve hanno non solo lo stesso valore ma anche la stessa pendenza (derivata prima); infatti la derivata della cubica è $3x^2 - 2x$ che per x = 1, vale 3 - 2 = 1, che è anche il coefficiente angolare della retta.
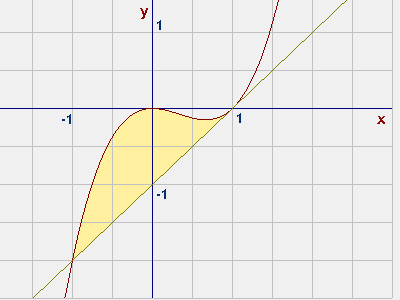
Si veda anche il disegno a lato.
Vi è quindi una sola regione di piano delimitata dalle due curve; per calcolarne l'area occorre calcolare l'integrale definito tra -1 e 1 della differenza tra la cubica e la retta:
$ \int^1_{-1} (x^3 - x^2 - x + 1){dx} = [x^4/4 - x^3/3 - x^2/2 + x]^1_{-1} = (1/4 - 1/3 - 1/2 + 1) - (1/4 + 1/3 - 1/2 - 1) = -1/3 + 1 -1/3 + 1 = 4/3 $
L'area tra le due curve vale quindi 4/3.