

|
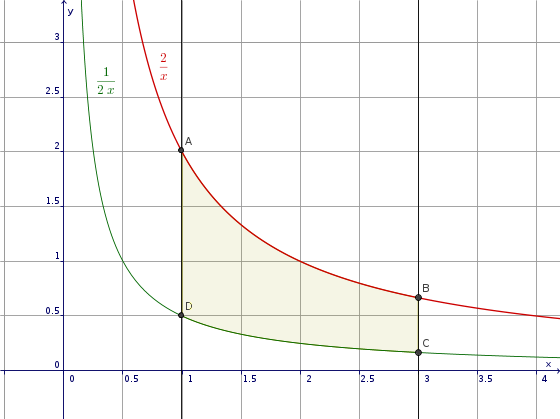
Calcolare l'area compresa tra le seguenti funzioni tra le due rette $x=1 ; x= 3$:
$$ \begin{array} \\ y = \frac{2}{x} \\ y = \frac{1}{2x} \end{array} $$
Si tratta di due iperboli. Il problema equivale a quello di calcolare il lavoro nel piano $Vp$ di un ciclo termodinamico formato da due isoterme e due isocore.
In questo caso non è necessario trovare punti comuni, i due estremi di integrazioni sono dati dal problema. Per calcolare l'area della regione di piano basta calcolare l'integrale definito tra 1 e 3 della differenza tra l'iperbole superiore ($ y = \frac{2}{x}$) e quella inferiore ($ y = \frac{1}{2x} $):
$ \int^{3}_{1}\left( \frac{2}{x} - \frac{1}{2x} \right)dx = \\ [2 \ln{x} - \frac{1}{2} \ln{x}]^3_{1} = (2 \ln{3} - 0,5 \ln{3}) - (0 - 0) = 1,5 \ln{3} \approx 1,647918 $
L'area tra le due curve vale quindi circa 1,647918.