

|
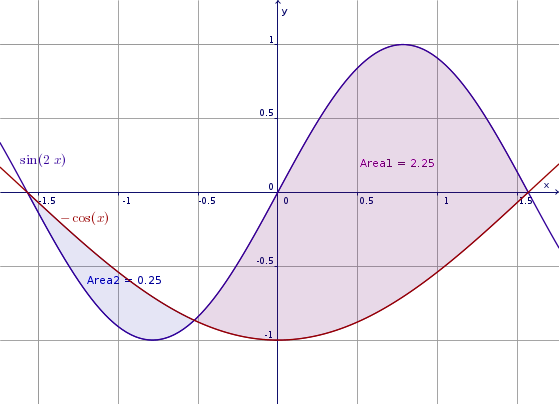
Calcolare una delle aree comprese tra le seguenti funzioni goniometriche:
$$ \begin{array} \\y = \sin(2x) \\ y = -\cos(x) \end{array} $$
Si tratta di un sinusoide con periodo dimezzato a $π$ e del cosinusoide ribaltato rispetto all'asse delle x.
Innanzitutto troviamo le intersezioni tra le due curve cosa che equivale a risolvere l'equazione:
$ \sin(2x) = -\cos(x) $
Ricordando la formula di duplicazione del seno, l'equazione diventa:
$ 2\sin{x}\cos(x) + \cos(x) = 0 $
e mettendo in evidenza $\cos{x}$ :
$ \cos(x)(2\sin{x} + 1) = 0 $
quindi considerando i due fattori $\cos{x}$ e $(2\sin{x} + 1)$ abbiamo due soluzioni:
$ \cos(x) = 0 → x = \frac{π}{2} + kπ \\ \sin{x} = -\frac{1}{2} → x = -\frac{π}{6} + 2kπ ; x = -\frac{5}{6}π + 2kπ$
Considerando le due soluzioni più vicine all'origine possiamo calcolare l'area tra $-\frac{5}{6}π$ e $\frac{π}{2}$:
$ \int^{\frac{π}{2}}_{-\frac{π}{6}} \left( \sin(2x) + \cos(x) \right)dx = \\ [-\frac{1}{2}\cos(2x) + \sin{x}]^{\frac{π}{2}}_{-\frac{π}{6}} = \left( \frac{1}{2} + 1 \right) - \left( -\frac{1}{4} - \frac{1}{2} \right) = \frac{9}{4} = 2,25 $
L'area tra le due curve vale quindi esattamente 2,25; può apparire strano che l'area tra due curve non algebriche e tra due estremi irrazionali anzi trascendenti come $-\frac{π}{6}$ e $x = \frac{π}{2}$ sia un numero razionale ma la cosa è perfettamente possibile così come è possibile che la somma di due irrazionali sia razionale.
Consideriamo ora l'area tra $-\frac{π}{2}$ e $-\frac{5}{6}π$; in questo intervallo il cosinusoide è la curva superiore, se vogliamo un risultato positivo occorre scambiare le due funzioni; ecco il calcolo:
$ \int^{-\frac{π}{6}}_{-\frac{π}{2}} \left(-\cos(x) - \sin(2x) + \right)dx = \\ [- \sin{x} +\frac{1}{2}\cos(2x) ]^{-\frac{π}{6}}_{-\frac{π}{2}} = \left( \frac{1}{2} - \frac{1}{4} \right) - \left( -1 + 1 \right) = \frac{1}{4} = 0,25 $
L'area tra le due curve vale quindi esattamente 0,25, un numero razionale come per l'altra area.