

|
Gli integrali oltre che a calcolare l'area sottesa a una curva tra due estremi, permettono di calcolare l'area delimitata da una o più curve.
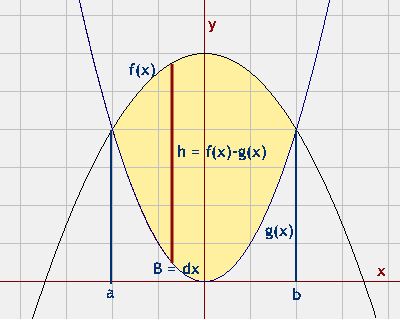
Consideriamo la figura a lato e l'area compresa tra le due curve di equazione $y = f(x)$ e $y = g(x)$; l'area può vedersi come la somma infinita dei rettangolini infinitesimi, come quello indicato in figura in color rosso scuro.
Questi rettangolini hanno base infinitesima $ dx $ e altezza data dalla differenza tra la curva superiore $f(x)$ e quella inferiore $g(x)$. L'area del rettangolino infinitesimo è allora $(f(x) - g(x)){dx}$ e l'area totale tra le rette $x = a$ e $x = b$ è data dall'integrale:
$ \int^{b}_{a} {f(x) - g(x)}dx $
calcolato tra i due estremi $a$ e $b$. Se si conoscono gli integrali indefiniti $F(x)$ $G(x)$ allora è:
$ \int^{b}_{a} {f(x) - g(x)}dx = [F(b)-G(b)] - [F(a)-G(a)]$ o anche $ [F(b)-F(a)] - [G(b)-G(a)]$ che è in sostanza l'area sottesa alla funzione superiore meno l'area sottesa alla funzione inferiore.
Se, come nel caso di polinomi, è facile semplificare $h(x)=f(x)-g(x)$ e calcolare l'integrale indefinito $ H(x) = \int{h(x)}$ è:
$ \int^{b}_{a} {h(x)}dx = H(b) - H(a)$
Questa tecnica è spesso chiamata area per fili: infatti è un po' come tirare infiniti fili verticali infinitesimi tra la curva superiore e quella inferiore e quindi sommare le infinite aree infinitesime di tutti questi fili, ovverosia calcolare l'integrale. Si intende che ogni filo (segmento) è lungo $f(x)-g(x)$
Il calcolo di $a$ e $b$ richiede naturalmente la soluzione del sistema tra le due funzioni, ovvero la soluzione dell'equazione $f(x) - g(x) = 0$. La difficoltà di questa equazione può naturalmente essere molto varia, da una banale equazione algebrica di secondo grado, a equazioni di grado superiore o trascendenti.
Calcolare l'area tra le due funzioni (parabole):
$ f(x) = -\frac{x^2}{2} +6 \\ g(x) = x^2 $
Risolvendo il sistema, qui molto semplice, si ricavano due soluzioni $ x=-2 \; x =+2 $
Si tratta di calcolare l'integrale della differenza tra la funzione superiore e la inferiore:
$ \int_{-2}^{+2} (-\frac{x^2}{2} +6 - x^2){dx} = \int_{-2}^{+2} (-\frac{3}{2}x^2 +6 ){dx} = \left [-\frac{x^3}{2} + 6x \right]_{-2}^{+2} = \left (-\frac{8}{2} + 12 \right) - \left(\frac{8}{2} - 12 \right) = 8 + 8 = 16$
L'area compresa tra le due parabole è quindi uguale a 16.
Una verifica veloce consiste nel conteggio approssimato dei quadratini, per esempio contare quelli che sono in maggioranza compresi nell'area. Ovviamente non ci si può attendere un risultato molto preciso, ma la verifica è utile per rifiutare risultati molto diversi dal conteggio dei quadratini.