

| $ D_x {f(x)g(x)} = f'(x)g(x) + f(x)g'(x) $ | |
| Controesempio | Dimostrazione della formula |
|---|---|
|
A differenza di quanto accade per la somma (la derivata della somma è uguale alla somma delle derivate) la derivata del prodotto NON è il prodotto delle derivate. Per verificarlo consideriamo come controesempio la funzione $ y = (x^2 - 1)(2x + 1) $ che svolgendo il prodotto equivale al polinomio $ y = 2x^3 + x^2 - 2x - 1 $ la cui derivata è $ y' = 6x^2 + 2x - 2 $ Le derivate dei due fattori sono rispettivamente 2x e 2, il cui prodotto è 4x, nulla a che fare con la derivata calcolata sopra. Basta questo controesempio per rendersi conto che la derivata del prodotto NON è il prodotto delle derivate. Fu Leibniz a trovare la regola di derivazione per il prodotto di due funzioni, che per questo porta il suo nome. Applicando la regola di Leibniz si ha: $ y' = 2x(2x + 1) + (x^2 - 1)2 = 4x^2 + 2x + 2x^2 - 2 = 6x^2 + 2x - 2 $ risultato che coincide con quello ricavato sopra. |
Consideriamo due funzioni $ u = f(x) $ e $ v = g(x) $ e il loro prodotto $ y = h(x) = uv = f(x)g(x) $. Incrementiamo $ u $ e $ v $ di un infinitesimo e di conseguenza anche y. Dimostrazione 1 usando la definizione di derivata: $ D_x f(x)g(x) = st \left ( \frac{h(x+dx)-h(x)}{dx} \right) = st \left ( \frac{(u+du)(v+dv)-uv}{dx} \right) = $ $\require{cancel} st \left ( \frac{\cancel{uv} + v{du} + u{dv} +{du} {dv}-\cancel{uv}}{dx} \right) = st \left ( \frac{v{du} + u{dv} +{du} {dv}}{dx} \right) = $ $ = st \left ( {v \frac{du}{dx} + u \frac{dv}{dx} + \frac{du}{dx}{dv}} \right) = u' v + u v'$ o anche ricordando che u = f(x) e v = g(x) $ D_x f(x)g(x) = f'(x)g(x) + f(x)g'(x) $ Dimostrazione 2 usando gli infinitesimi: 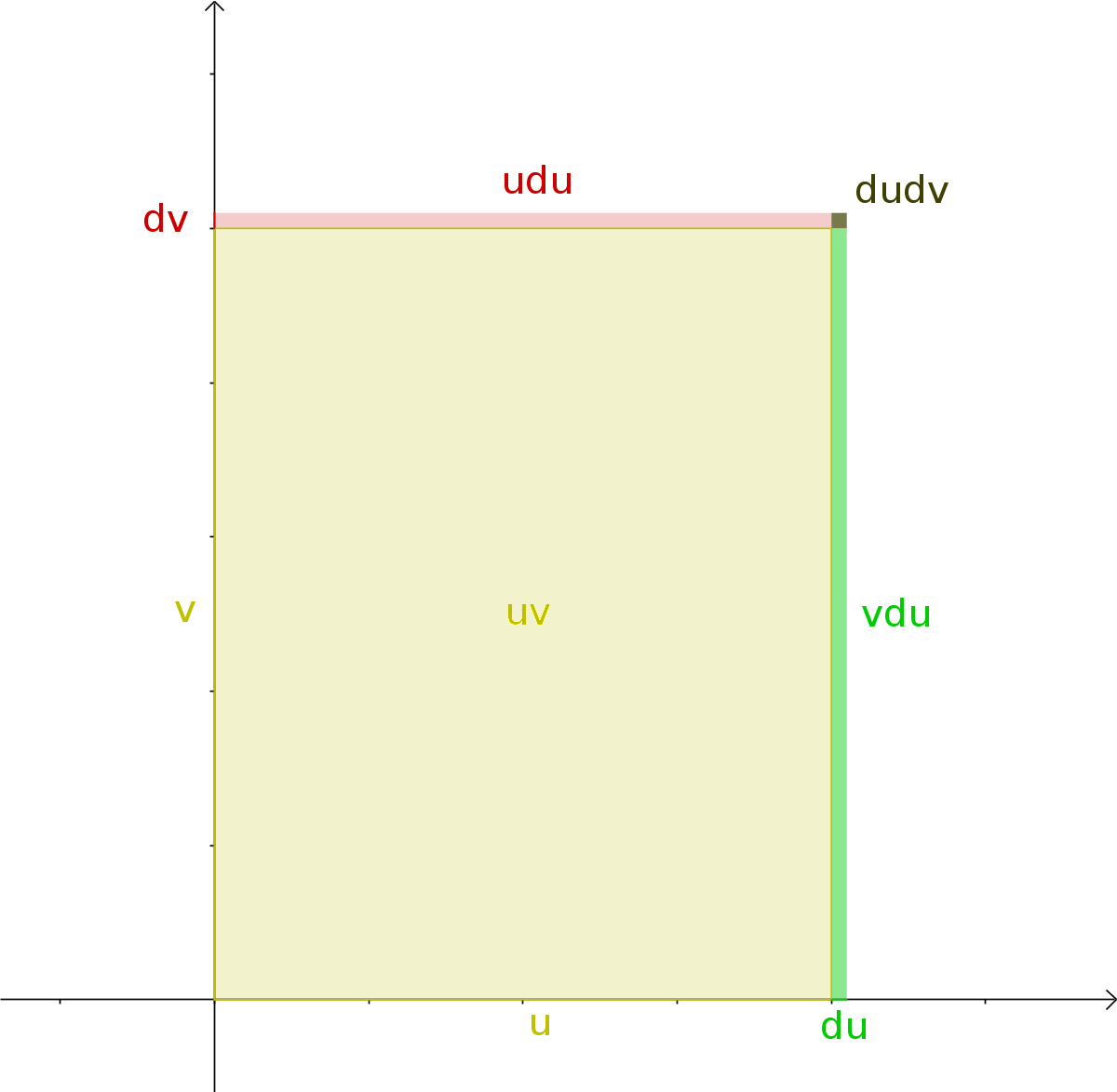
$ \begin{cases} y = uv \\ y + dy = (u + du)(v + dv) \end{cases} $ Sostituendo y nella seconda e svolgendo il prodotto con la proprietà distributiva: $ uv + dy = uv + u {dv} + v {du} + {du} {dv} $ e quindi eliminando $ uv $ e dividendo tutto per $ dx $: $ \frac{dy}{dx} = u \frac{dv}{dx} + \frac{du}{dx}v + \frac{du}{dx}{dv} $ ricordando ora che la derivata è la parte standard di $ \frac{dy}{dx} $ e che l'ultimo termine sopra è un infinitesimo, si ottiene: $ D_x {uv} = uv' + u'v $ risultato equivalente al precedente. Per ricordarla basta osservare che si tratta della somma di due prodotti misti la derivata della prima funzione per la seconda più la prima funzione per la derivata della seconda. L'ordine dei due prodotti non ha ovviamente alcuna importanza. Un'interpretazione geometrica di questo risultato è mostrata nel disegno qui accanto; l'incremento del prodotto $uv$, area del rettangolo è dato dalla somma dei due rettangoli laterali infinitesimi $u{dv}$ e $v{du}$. Il rettangolino ${du} \times {dv}$ è infinitesimo del secondo ordine e quindi trascurabile rispetto ai rettangoli laterali. |
| Funzione | Derivate di f(x) e g(x) | Derivata di f(x).g(x) |
|---|---|---|
| $ y = (x - 1)(x - 2) \\ f(x) = x - 1 \\ g(x) = x - 2 $ | $ f'(x) = 1 \\ g'(x) = 1 $ | $ D_x {(x -1)(x - 2)} = 1(x - 2) + (x - 1)1 = x - 2 + x - 1 = 2x - 3 $ |
| $ y = (2x - 1)(2 - x^2) \\ f(x) = 2x - 1 \\ g(x) = 2 - x^2 $ | $ f'(x) = 2 \\ g'(x) = -2x $ | $ D_x {(2x - 1)(2 - x)} = (2x - 1)(-2x) + 2 (2 - x^2) = -4x^2 + 2x + 4 - 2x^2 = -6x^2 + 2x + 4 $ |
Calcolare la derivata delle seguenti funzioni