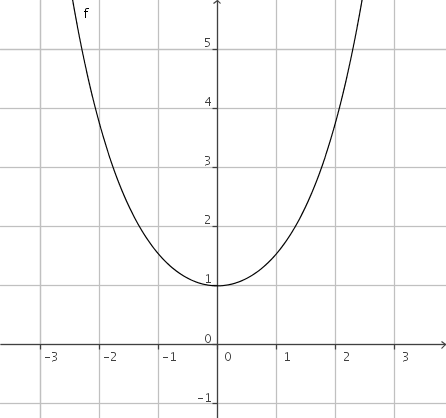
Studio del coseno iperbolico
$$ y = \frac{e^x + e^{-x}}{2} = \cosh(x) $$
Il coseno iperbolico è per definizione la media aritmetica tra $e^x$ ed $e^{-x}$.
Il simbolo più usato è $\cosh(x)$ ma si trova anche l'abbreviazione $ch(x)$.
-
Insieme di definizione: le funzioni esponenziali $e^x$ ed $e^{-x}$ sono definite per ogni x reale, e quindi è I = R.
-
Simmetrie: cambiando x in -x la funzione non cambia di valore; si tratta quindi di una funzione pari, simmetrica rispetto all'asse delle y.
-
Ricerca degli zeri della funzione, ovvero soluzione dell'equazione $\cosh(x)$ = 0.
Le funzioni $e^x$ ed $e^{-x}$ non si annullano mai e così sarà a maggior ragione per la loro somma; dunque non ci sono zeri.
-
Studio del segno della funzione, in base a quanto appena detto è $\cosh(x) > 0$ sempre.
-
Calcolo della derivata.
La funzione è la metà della somma di due funzioni e quindi la derivata è la metà della somma delle derivate di $e^x$ ed $e^{-x}$, che sono rispettivamente $e^x$ e $-e^{-x}$:
$ y' = \frac{e^x - e^{-x}}{2} = \sinh(x) $
Si tratta del seno iperbolico. La derivata del coseno iperbolico è quindi il seno iperbolico.
La derivata seconda è con procedimento del tutto analogo:
$ y'' = \frac{e^x - (-e^{-x})}{2} = \frac{e^x + e^{-x}}{2} = \cosh(x) $
In altre parole la derivata seconda coincide con la funzione di partenza.
-
Ricerca dei massimi, dei minimi.
La derivata appena ottenuta si annulla quando si annulla $e^x = e^{-x}$. Due potenze con la stessa base sono uguali solo quando sono uguali gli esponenti e quindi si ha:
$ x = - x ; 2x = 0 ; x = 0 $
Per verificare se si tratta di un massimo o un minimo si può usare il primo metodo, quello
della disequazione 2x > 0; usando il solito schema:
0
2x -----------------------o+++++++++++++++++++++++++++++o
-\ + /
Dallo schema risulta evidente che c'è un minimo per x = 0, e y = 1.
Usando il secondo metodo (derivata seconda) dal fatto che la derivata seconda per x= 0 vale 1 segue che si tratta di un minimo.
-
Ricerca dei flessi.
Uguagliando a zero la derivata seconda ottenuta sopra si ha l'equazione: $\cosh(x) = 0$ ma come si è detto sopra $\cosh(x)$ è sempre positiva e non si annulla mai, dunque la funzione ha la concavità sempre rivolta verso l'alto e non ci sono flessi.
Riassumendo tutti questi risultati si ottiene il grafico riportato sopra, che ricorda quello della parabola. Questa curva è detta anche catenaria perché una catena appesa per i due estremi si dispone in questo modo.