I metodo per la ricerca dei punti di flesso

Il metodo si basa sul fatto che nei punti di flesso la derivata seconda deve essere nulla.

Si tratta quindi, prima di tutto, di calcolare la derivata f"(x) e quindi porre f"(x) = 0.

A differenza del II metodo il I metodo non richiede il calcolo di altre derivate, ma solo la soluzione della disequazione f"(x) > 0.

Le soluzioni della disequazione ci dicono dove la concavità è verso l'alto (f"(x) > 0) e dove verso il basso (f"(x) > 0). Osservando lo schema si può facilmente decidere se si tratta di un punto di flesso o di un punto piatto.

se la derivata seconda è positiva prima e negativa dopo il punto si ha un flesso.
se la derivata seconda è negativa prima e positiva dopo il punto si ha un flesso.
se la derivata seconda è positiva sia prima sia dopo si ha un punto piatto.
se la derivata seconda è negativa sia prima sia dopo si ha un punto piatto.

Si vedano comunque i seguenti tre esempi per comprendere meglio il metodo.

Esempio 1

                      0
x > 0  ---------------o++++++++++++++++
	       /\	          \/

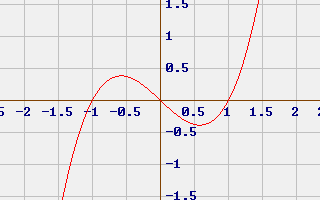
Sia data la funzione y = x³ - x

Le derivate sono:

y' = 3x² - 1
y" = 6x

Uguagliando a zero si ha l'equazione 6x = 0, e una sola soluzione x = 0. La disequazione è rappresentata dallo schema a destra.

Osservando lo schema si vede che la concavità cambia per x = 0 e quindi si ha il flesso Flex(0;0) coincidente con l'origine; la derivata prima 3x² - 1 vale -1 per x = 0 e quindi il flesso ha tangente decrescente.

Esempio 2

                      -√(1/6)   +√(1/6)
x − √(1/6) > 0  -----------------o+++++++++++
x + √(1/6) > 0  ---------o+++++++++++++++++++
                    +          -          +
                   \ /        / \        \ /

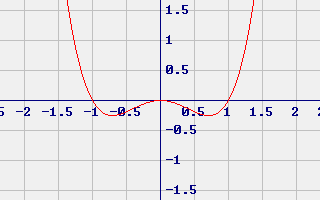
Sia data la funzione y = x⁴ - x².

Le derivate sono:

y' = 4x³ - 2x
y" = 12x² - 2

Uguagliando a zero si ha l'equazione 12x² - 2, e le due soluzioni sono x = ±√(1/6) ≈ 0,4

Osservando lo schema si vede che la concavità cambia per x = -√(1/6) e per x = +√(1/6) dunque ci sono due flessi:

Flex1(-√(1/6); -5/36) e Flex2(+√(1/6); -5/36).

Calcolando f'(-√(1/6)) si trova -√(1/216) -2.(-√(1/6)) ~ 0,74 dunque il primo flesso è crescente; analogamente si ricava che il secondo flesso vale circa -0,74 e quindi è decrescente.