Flessi di una curva

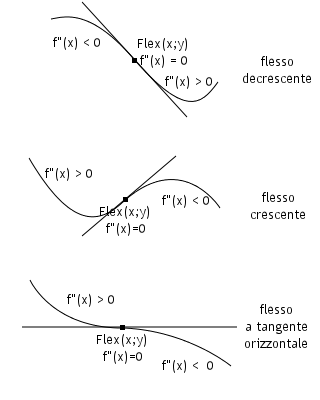
Intuitivamente un punto di flesso è un punto nel quale cambia la concavità: immaginando di camminare lungo la curva è il punto nel quale cambia la curvatura: se prima si girava verso destra, dopo si gira verso sinistra o viceversa.

Il flesso è dunque un punto nel quale la concavità non è né positiva né negativa e quindi nulla. In altre parola la derivata seconda deve essere nulla.

$$f''(x) = 0$$

Di per sé però la condizione $f''(x) = 0$ non è sufficiente ad assicurare la presenza di un flesso; potrebbe anche trattarsi di un massimo o minimo piatto e cioè con derivate prima e seconda entrambe nulle.

La ricerca dei flessi è del tutto analoga a quella dei massimi e minimi sostituendosi alla derivata prima la derivata seconda.

Si tratta di:

1. Calcolare la derivata seconda della funzione $f''(x)$.
2. Risolvere l'equazione $f''(x) = 0$.
3. Discutere le soluzione dell'equazione per decidere se si tratta realmente di un flesso.

• I metodo per la ricerca dei punti di flessi: consiste nel risolvere la disequazione $f''(x) > 0$.
• II metodo per la ricerca dei punti di flesso: consiste nell'esaminare il segno della derivata terza $f'''(x)$ ed eventualmente delle derivate successive.