Il metodo si basa sul fatto che nei punti di flesso la derivata seconda deve essere nulla e la prima derivata successiva che non si annulla deve avere ordine dispari; se viceversa ha ordine pari non ci sarà flesso.
Si tratta quindi di calcolare la derivata $f''(x)$, risolvere $f''(x) = 0$ e per ogni soluzione $x_i$ calcolare $f'''(x_i)$.
Si vedano comunque i seguenti tre esempi per comprendere meglio il metodo.
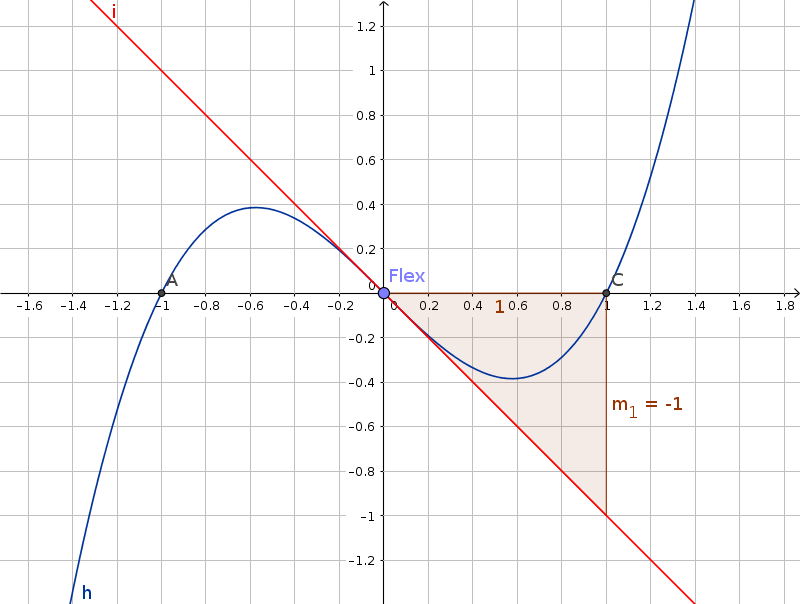
Sia data la funzione $y = x^3 - x$
Le derivate sono:
$ y' = 3x^2 - 1 \\ y'' = 6x \\y''' = 6 $
Uguagliando a zero si ha l'equazione $6x = 0$, e una sola soluzione $x = 0$; la derivata terza è uguale a $6$, quindi comunque positiva: si ha il flesso $flex(0;0)$ coincidente con l'origine; la derivata prima $3x^2 - 1$ vale $-1$ per $x = 0$ e quindi il flesso ha tangente decrescente.
Clic sulla freccia per vedere il grafico della funzione nelle vicinanze dell'origine:(→)
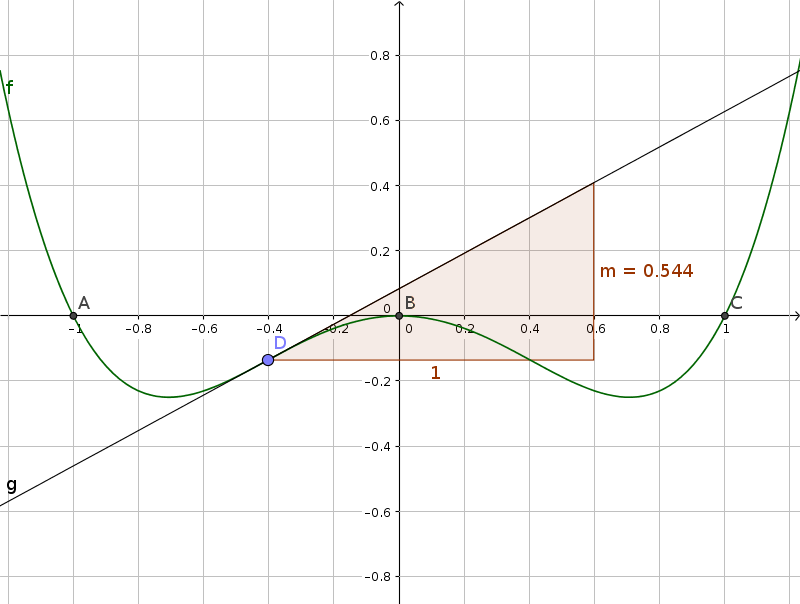
Sia data la funzione $y = x^4 - x^2$.
Le derivate sono:
$ y' = 4x^3 - 2x \\ y'' = 12x^2 - 2 \\ y''' = 24x$
Uguagliando a zero la derivata seconda si ha l'equazione $12x^2 - 2$, e le due soluzioni sono $x = \pm\sqrt{\frac{1}{6}} \approx\pm 0.408$
La derivata terza $24x$ ha lo stesso segno di $x$, dunque è negativa per $x = -\sqrt{\frac{1}{6}}$ e positiva per $x = \sqrt{\frac{1}{6}}$; in ogni caso è diversa da zero e quindi si tratta di due flessi, entrambi con $y = \frac{1}{36} - \frac{1}{6} = -\frac{5}{36}$:
$flex_1 \left( -\sqrt{\frac{1}{6}} ; - \frac{5}{36} \right) \\ flex_2 \left( \sqrt{\frac{1}{6}} ; - \frac{5}{36} \right)$.
Calcolando la derivata prima (e cioé la pendenza della curva, si ha: $f'\left(-\sqrt{\frac{1}{6}}\right) = -4 \sqrt{\frac{1}{216}} + 2 \sqrt{\frac{1}{6}} \approx 0.544 $ dunque il primo flesso è crescente; analogamente si ricava che il secondo flesso vale circa $-0,544$ e quindi è decrescente, pendenza $m=-1$.
Clic sulla freccia per vedere il grafico della funzione nelle vicinanze dell'origine:(→)