

|
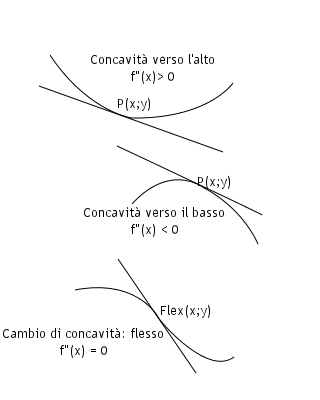
Intuitivamente la concavità di una curva è la parte interna della curva.
In un riferimento cartesiano la concavità è considerata positiva se rivolta verso l'alto, negativa se rivolta verso il basso.
Per stabilire se in un dato punto $P(x_0, y_0)$ la concavità è positiva o negativa, occorre esaminare il comportamento della curva in un intorno infinitesimo della medesima, in altre parole per $x_0 + dx$ e $x_0 - dx$.
Se sia per $x_0 - dx$ sia per $x_0 + dx$ la curva è al di sopra della tangente, allora la concavità è positiva.
Se sia per $x_0 - dx$ sia per $x_0 + dx$ la curva è al di sotto della tangente, allora la concavità è negativa.
Dal momento che l'equazione della tangente è $y = f(x_0) + f'(x_0)(x - x_0)$ la condizione perchè la curva abbia concavità positiva si può scrivere come segue:
$ f(x_0 - dx) > f(x_0) - f'(x_0){dx} \\f(x_0 + dx) > f(x_0) + f'(x_0){dx}$
che equivale a:
$\frac{(f(x_0 - dx) - f(x_0))}{dx} > - f'(x_0) \rightarrow \frac{(f(x_0) - f(x_0 - dx))}{dx} < f'(x_0) \frac{f(x_0 + dx) - f(x_0)}{dx} > + f'(x_0)$che equivale a:
$f'(x_0 - dx) < f'(x_0)\\f'(x_0 + dx) > f'(x_0)\\f'(x_0 - dx) < f'(x_0) < f'(x_0 + dx)$
In altre parola concavità verso l'alto equivale a dire derivata prima crescente e quindi derivata seconda maggiore di zero. Analogamente si ricava che concavità verso il basso equivale a dire derivata prima decrescente e quindi derivata seconda minore di zero.
$f"(x_0) > 0$ concavità verso l'alto in $x_0$
$f"(x_0) < 0$ concavità verso il basso in $x_0.$
Che cosa accade se viceversa la curva sta da parti opposte della tangente?
Se per $x_0 - dx$ e per $x_0 + dx$ la curva sta da parti opposte della tangente, P è un punto di flesso.
Un flesso è quindi un punto di minimo o di massimo della derivata prima e quindi un punto nel quale la derivata seconda si annulla.