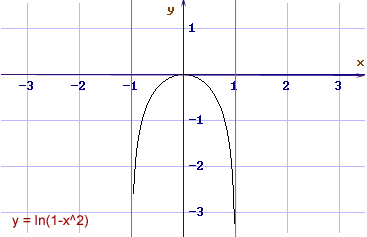
| Studiare la funzione logaritmica |
|---|
y = ln(1 - x²)
|
Vediamo i singoli passi dello studio
- Insieme di definizione il logaritmo è definito quando il suo argomento è maggiore
di zero. Si tratta quindi di risolvere la disequazione:
1 - x^2 > 0
(1 - x).(1 - x) > 0
si tratta quindi di discutere i due fattori (1 - x) e (1 + x) sul consueto diagramma:
-1 +1
1 - x ++++++++++++++++o-----------------
1 + 1 ---------o++++++++++++++++++++++++
- + -
risulta evidente allora che la funzione è definita nell'intervallo ]-1, 1[ = {x | -1 < x < 1}
- Ricerca di eventuali asintoti verticali per x = -1 e x = +1 la funzione non è definita.
- Ricerca degli zeri della funzione, ovvero soluzione dell'equazione ln(1-x2) = 0.
Il logaritmo si annulla quando l'argomento vale 1. Dunque basta risolvere l'equazione:
1 - x2 = 1
- x2 = 0
x = 0
Dunque la funzione ha uno zero nell'origine.
- Studio del segno della funzione, ovvero soluzione della disequazione ln(1-x2) >= 0.
La disequazione si riduce subito alla
1 - x2 >= 1
- x2 >= 0
Ma - x2 è sempre negativo dunque la funzione è sempre negativa (sotto l'asse delle
x) salvo per il caso x = 0 già studiato.
- Calcolo della derivata.
La funzione è una funzione composta, e la derivata è in base alla
corrispondente regola.
y = ln(t)
t = 1 - x2
dy 1 dt dy 1 -2x
---- = --- ; ---- = -2x ==> ---- = -2x.--- = -------
dt t dx dx t 1 - x2
- Ricerca dei massimi, dei minimi e dei flessi.
La derivata appena ottenuta si annulla quando si annulla il numeratore -2x, dunque per x = 0.
Per verificare se si tratta di un massimo o un minimo si può usare il primo metodo, quello
della disequazione f'(x) > 0; usando il solito schema:
-1 0 +1
-2x +++++++++++++++++++++++++++++o-----------------------
1 - x -------------------------------------o+++++++++++++++
1 + x ++++++++++++++++++++++o-------------------------
- + / -\ +
Dallo schema risulta evidente che c'è un massimo nell'origine.
Riassumendo tutti questi risultati si ottiene il grafico riportato sopra.