y = ln(1 - x3)

Grafico della funzione

Vediamo i singoli passi dello studio

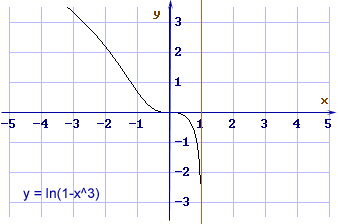
1. Insieme di definizione il logaritmo è definito quando il suo argomento è maggiore di zero. Si tratta quindi di risolvere la disequazione:

   1 - x^3 > 0
   
   (1 - x).(1 + x + x2) > 0
   

   il secondo fattore è un falso quadrato che è sempre maggiore di zero. Tutto si riduce quindi al fattore 1 - x

                         +1
   1 - x  +++++++++++++++o----------------
                  +              -
   

   e risulta evidente allora che la funzione è definita nell'intervallo ]-∞, 1[ = {x | x < 1}
2. Ricerca di eventuali asintoti verticali per x = +1 la funzione vale ln(0) che è meno infinito. C'è dunque un asintoto verticale x = +1.
3. Ricerca degli zeri della funzione, ovvero soluzione dell'equazione ln(1-x³) = 0. Il logaritmo si annulla quando l'argomento vale 1. Dunque basta risolvere l'equazione:

   1 - x3 = 1
   
   - x3 = 0
   
   x = 0
   

   Dunque la funzione ha uno zero nell'origine.
4. Studio del segno della funzione, ovvero soluzione della disequazione ln(1-x³) >= 0. La disequazione si riduce subito alla

   1 - x3 >= 1
   - x3 >= 0
   - x >= 0
   x <= 0
   
                     0    +1
   x  +++++++++++++++o-----
              +         -
   

   Dunque la funzione è negativa per x > 0, negativa per x < 0.
5. Calcolo della derivata. La funzione è una funzione composta, e la derivata è in base alla corrispondente regola.

   y = ln(t)
   t = 1 - x3
   
    dy     1       dt               dy          1      -3x2
   ---- = ---  ;  ---- = -3x2  ==>  --- = -3x2.--- = -------
    dt     t       dx               dx          t     1 - x³
   

6. Ricerca di massimi e minimi. La derivata appena ottenuta si annulla quando si annulla il numeratore -3x², dunque per x = 0. Per verificare se si tratta di un massimo o un minimo si può usare il primo metodo, quello della disequazione f'(x) > 0; usando il solito schema:

                               0      +1
   -3x²       -----------------o------------------------
   1 - x      +++++++++++++++++++++++++o----------------
   1 + x + x² ++++++++++++++++++++++++++++++++++++++++++
                         -\                   +
   

   Dallo schema risulta che la funzione è sempre decrescente nel suo insieme di definizione (x < 1) salvo nell'origine dove la derivata prima si annulla. Dunque per x = 0 c'è un flesso a tangente orizzontale.
7. Ricerca di ulteriori punti di flesso. Occorre innanzitutto calcolare la derivata seconda, cosa che richiede la regola di derivazione del quoziente.

         -3x²
   y' = ---------
         1 - x³
   
         -6x(1 - x³) - (-3x²)(-3x²)    -6x + 6x4 - 9x4
   y" = --------------------------- = ----------------
              (1 - x³)²                   (1 - x³)²
         -6x - 3x4      -3x(2 + x³)
   y" = ------------ = -------------
          (1 - x³)²      (1 - x³)²
   

                        -³√2      0     +1
   -3x       +++++++++++++++++++++o-------------------
   2 + x³    ------------o++++++++++++++++++++++++++++
   (1 - x³)² +++++++++++++++++++++o+++++++++++++++++++
   Concavità:        -        +         - 
   

   Dallo schema risultano due valori per i quali la y" si annulla e cambia di segno e quindi di concavità; ci sono dunque due flessi: per x = 0 quello a tangente orizzontale già trovato. Per x = -³√2 c'è un ulteriore punto di flesso decrescente, di coordinate F (-³√2; ln(3)) = (-1,26; 1,09)