y = ln(x2 - 1)

Grafico della funzione

Vediamo i singoli passi dello studio

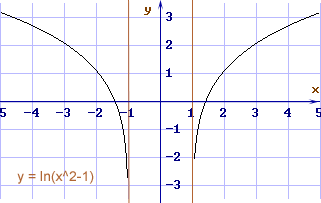
1. Insieme di definizione il logaritmo è definito quando il suo argomento è maggiore di zero. Si tratta quindi di risolvere la disequazione:

   x^2 - 1> 0
   
   (x - 1).(x - 1) > 0
   

   si tratta quindi di discutere i due fattori (1 - x) e (1 + x) sul consueto diagramma:

                  -1     +1
   x - 1  ----------------o++++++++++++++++
   x + 1  ---------o+++++++++++++++++++++++
             +         -        +
   

   risulta evidente allora che la funzione è definita nell'intervallo ]-∞, -1[ U ]+1, ∞[ = {x | x < -1 v x > +1}
2. Ricerca di eventuali asintoti verticali per x = -1 e x = +1 la funzione vale ln(0) che è meno infinito. Ci sono dunque due asintoti verticali x = -1 e x = +1.
3. Ricerca degli zeri della funzione, ovvero soluzione dell'equazione ln(x² - 1) = 0. Il logaritmo si annulla quando l'argomento vale 1. Dunque basta risolvere l'equazione:

   x² - 1 = 1
   
   x2 = 2
   
   x = ±√2
   

   Dunque la funzione ha due zeri -√2 e +√2.
4. Studio del segno della funzione, ovvero soluzione della disequazione ln(1-x²) >= 0. La disequazione si riduce subito alla

   x² - 1 >= 1
   
   x² - 2 >= 0
   
   (x - √2)(x + √2) >= 0
   

   e usando il solito schema:

                  -√2     +√2
   x - √2  ----------------o++++++++++++++++
   x + √2  ---------o+++++++++++++++++++++++
             +         -        +
   

   la funzione è quindi positiva all'esterno dell'intervallo ]-√2, +√2[
5. Calcolo della derivata. La funzione è una funzione composta, e la derivata è in base alla corrispondente regola.

   y = ln(t)
   t = x² - 1
   
    dy     1       dt              dy        1      2x
   ---- = ---  ;  ---- = 2x  ==>  ---- = 2x.--- = --------
    dt     t       dx              dx        t     x² - 1
   

6. Ricerca di massimi, minimi. La derivata appena ottenuta si annulla quando si annulla il numeratore 2x, dunque per x = 0. Per verificare se si tratta di un massimo o un minimo si può usare il primo metodo, quello della disequazione f'(x) > 0; usando il solito schema:

                          -1      0      +1
   2x    -------------------------o+++++++++++++++++++
   x - 1 ---------------------------------o+++++++++++
   x + 1 ------------------o++++++++++++++++++++++++++
                  -\          +      -        +/
   

   Dallo schema risulta evidente che non ci sono massimi o minimi. Tra -1 e +1 infatti la funzione non è definita.