

|
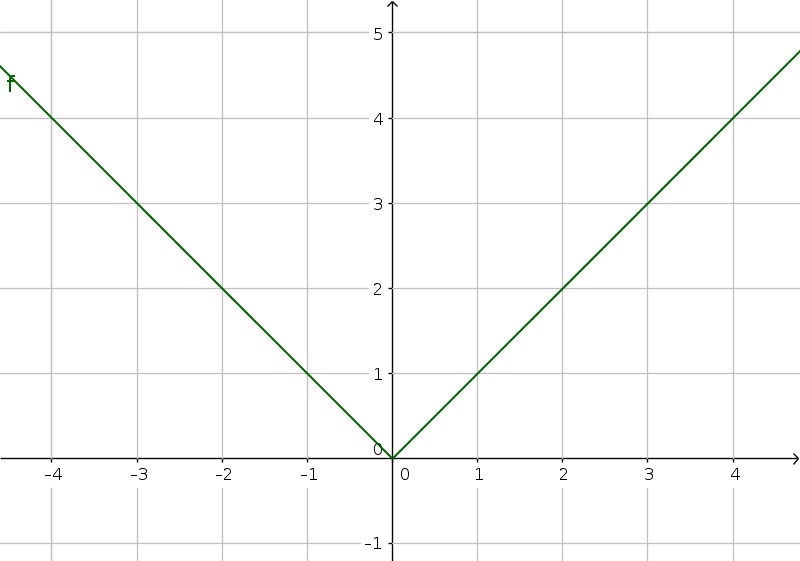
La funzione valore assoluto è quella che dato in ingresso un qualsiasi numero reale, ne restiuisce il valore positivo, senza segno; formalmente può essere definita come segue, distinguendo il caso in cui $x$ è negativo da quello in cui è positivo. $$ \begin{cases} x \ge 0 \rightarrow y = x \\x \lt 0 \rightarrow y = -x \end{cases}$$La funzione è definita per ogni numero reale quindi il dominio è $\mathbb{R}$ (si può estendere a $\mathbb{R}^{*}$). Si indica con due barrette verticali $y = |x|$; in molti ambienti informatici si scrive $abs(x)$. Il punto più interessante è l'origine, che viene chiamata punto angoloso, un punto nel quale la pendenza cambia in modo brusco passando da $m=-1$ a $m=1$. La cosa può essere verificata calcolando formalmente la derivata che non è unica, dipende dal segno : $$ \begin{cases} x \gt 0 \rightarrow y' = st \left( \frac{|0+\epsilon| - |0|}{\epsilon} \right) = 1 \\x \lt 0 \rightarrow y' = st \left( \frac{|0-\epsilon| - |0|}{-\epsilon} \right) = -1 \end{cases}$$Si tratta della funzione segno, di cui al riquadro qui sotto. Per $x = 0$ la derivata è diversa a seconda che la si calcoli verso destra, nel qual caso si ha $\frac{dy}{dx} = \frac{dx}{dx} = 1$, o verso sinistra, nel qual caso si ha $\frac{dy}{dx} = \frac{-dx}{dx} = -1$ Si dice allora che la funzione non è derivabile per $x=0$. In generale si dice che una funzione non è derivabile per un certo valore $x_0$ quando il valore della derivata (parte standard) varia a seconda dell'infinitesimo usato (qui a seconda del segno) e quindi presenta salti; in altri termini la derivata presenta una discontinuità.
|
|
|
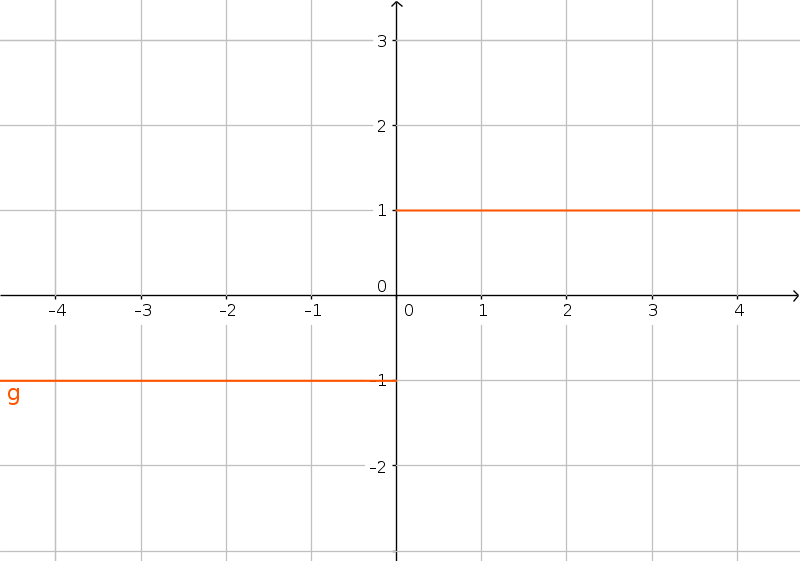
La funzione segno è quella che dato in ingresso un qualsiasi numero reale, restiuisce $1$ per valori positivi, $-1$ per i negativi; formalmente può essere definita come segue:. $$ \begin{cases} x > 0 \rightarrow y = +1 \\x < 0 \rightarrow y = -1 \end{cases} $$Risulta essere uguale al quoziente $\frac{|x|}{x}$, escludendo il caso ideterminato $x=0$ e quindi il dominio è $\mathbb{R}-\{0\}$. Viene spesso completata in $\mathbb{R}$ ponendo $f(0) = 0$. Questa funzione si scrive per lo più $ \DeclareMathOperator\sign{sgn} \sign(x)$. Nell'origine la funzione non è definita ma nella sua monade passa in modo brusco da $-1$ a $+1$. Si ha quindi una discontinuità non eliminabile, nel senso che anche assegnando un qualche valore per $x=0$ la funzione resta discontinua (vedi pagina Continuità, secondo esempio per dettagli). Possiamo comunque scrivere che: $$ \DeclareMathOperator\sign{sgn} D_x{|x|} = \sign{x}$$ fermo restando che la funzione non è derivabile per $x=0$. |
|