Il concetto di continuità in matematica è intuitivamente abbastanza semplice: una curva si dice continua se è possibile disegnarla senza mai staccare la matita dal foglio di carta. Non ci devono essere salti (o discontinuità).

Il concetto si può ovviamente applicare anche a funzioni di variabile reale $y = f(x)$. Intuitivamente una funzione $f(x)$ si dice continua se il suo grafico si può tracciare senza mai staccare la matita dalla carta, senza salti quindi.

Da questa definizione intuitiva si ricavano definizioni più rigorose; non staccare mai la matita dalla carta equivale a dire che a ogni sia pur piccolissimo incremento nella direzione dell'asse delle x deve corrispondere un altrettanto piccolo incremento nella direzione dell'asse y.

Se alla parola piccolissimo sostituiamo quella di infinitesimo otteniamo questa definizione:

Una funzione f(x) si dice continua a destra (a sinistra) in un punto P(x;y) se incrementando (o decrementando) x di un infinitesimo ε, anche la y aumenta al più di un infinitesimo ovvero che la parte standard di dy è 0.

Abbiamo quindi due tipi di continuità, a destra e a sinistra; quella a destra, per valori maggiori di x, è definita da questa condizione, con $ε$ infinitesimo positivo:

$ st \left( f(x + ε) - f(x) \right) = 0 $

La continuità a sinistra (valori minori) è definita da questa condizione:

$ st \left( f(x - ε) - f(x) \right) = 0 $

La continuità di una funzione si può anche definire usando il concetto di infinitamente vicino:

$ x_0 \simeq x_1 \implies f(x_0) \simeq f(x_1) $

A parole: se due numeri x₀ , x₁ sono infinitamente vicini allora lo sono anche le loro immagini f(x₀), f(x₁). Si noti che c'è una sottile differenza tra queste due formulazioni; nella prima infatti si sottintende che x sia un numero reale e x+ε iperreale, mentre nella seconda i due numeri $x_0 , x_1$ potrebbero anche essere entrambi iperreali. Perché siano perfettamente equivalenti si può per esempio imporre la condizione che $x_0$ sia reale.

Una funzione che non soddisfa questa condizione si dice discontinua nel punto P. Si dice anche che in P c'è una discontinuità. La discontinuità può essere a destra o a sinistra.

Se viceversa si ammette che $x_0$ e $x_1$ possano essere entrambi iperreali si definisce la cosiddetta continuità uniforme definizione che non sempre coincide con la precedente (vedi esempi qui sotto). Una funzione si dice quindi uniformemente continua se la condizione di sopra vale per qualsiasi coppia di iperreali.

La continuità uniforme è una proprietà globale della funzione, mentre la continuità in un punto è una proprietà del punto; e una stessa funzione può essere continua in un punto ma non in un altro.

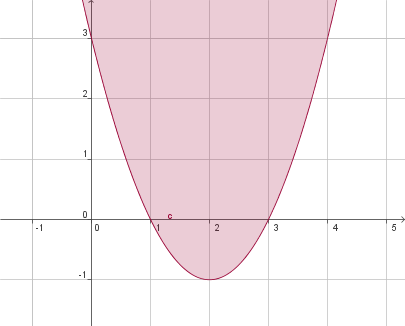
Una qualsiasi funzione algebrica intera (polinomio) P(x) è continua per ogni valore reale di x. Infatti $P(x+ε) - P(x)$ è sempre infinitesima; per esempio dato $P(x) = x^2 - 4x + 3 $ si ha:

$\require{cancel} ((x + ε)^2 - 4(x + ε) + 3) - (x^2 - 4x + 3) = \\ \cancel{x^2} + 2x {ε} + ε^2 - \cancel{4x} - 4ε + \cancel{3} - \cancel{x^2} + \cancel{4x} - \cancel{3} = \\ 2x{ε} - 4{ε} + {ε}^2$

che è appunto un infinitesimo, qualunque sia $x$; il fatto che il risultato sia infinitesimo dipende dal fatto che i termini non infinitesimi (qui $x^2 - 4x + 3$) si elidono a vicenda, lasciando solo termini infinitesimi. È facile convincersi che questo avviene per qualsiasi polinomio, dunque si tratta di un risultato generale: tutte le funzioni polinomie sono continue per ogni valore della x.

Una funzione polinomia è quindi continua in ogni suo punto a coordinate reali. Ma cosa avviene se si estende agli iperreali? È uniformemente continua?

È facire rendersi conto che per valori infinitamente grandi, la continuità viene meno; proviamo a calcolare l'incremento tra due numeri infinitamente grandi e infinitamente vicini tra di loro, p.es. $\omega$ e $\omega+\epsilon$:

$\require{cancel} ((ω + ε)^2 - 4(ω + ε) + 3) - (ω^2 - 4ω + 3) = \\ \cancel{ω^2} + 2ω {ε} + ε^2 - \cancel{4ω} - 4ε + \cancel{3} - \cancel{ω^2} + \cancel{4ω} - \cancel{3} = \\ 2ω{ε} - 4{ε} + {ε}^2 = 2 - 4{ε} + {ε}^2 \simeq 2$(*)

Qui a un incremento infinitesimo della x, corrisponde un salto non infinitesimo, infinitamente vicino a 2. Quindi la funzione non è uniformemente continua.

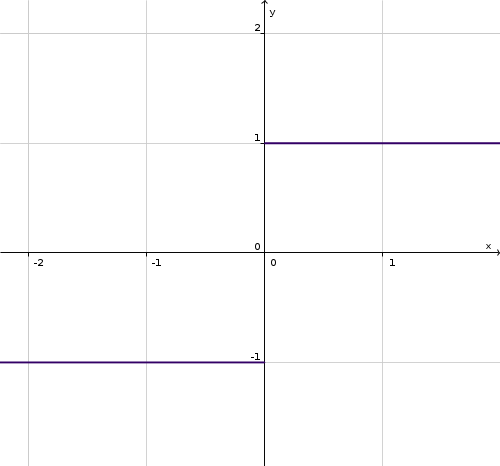
Come controesempio consideriamo la funzione y = Segno(x) così definita:

$ \begin{cases} f(x) = +1 \text{ per } x > 0 \\ f(x) = 0 \text{ per } x = 0 \\ f(x) = -1 \text{ per } x < 0 \end{cases}$

Nel punto P(0;0) (origine) la funzione non è continua infatti:

$ Segno(0+ε) - Segno(0) = 1 - 0 = 1 $

e 1 non è un infinitesimo! Che nell'origine ci sia una discontinuità è evidente anche dal disegno. Il risultato del calcolo ha un significato geometrico preciso: misura l'entità del salto.

La funzione è quindi discontinua a destra, e si verifica facilmente che è discontinua anche a sinistra.

Se invece definiamo la funzione f(x) = SegnoD(x) in modo leggermente diverso dalla Segno(x):

$ f(x) = +1 \text{ per } x > 0 \\ f(x) = -1 \text{ per } x \leq 0$

Nell'origine O(0;0) la funzione è discontinua a destra infatti:

$ SegnoD(0+ε) - SegnoD(0) = 1 - (-1) = 1+1 = 2 $

e quindi fa un salto di due unità; viceversa è continua a sinistra infatti:

$ SegnoD(0-ε) - SegnoD(0) = -1 - (-1) = 0 $

Una curiosità: se la funzione segno viene definita solo per numeri diversi da zero, se ha cioè dominio $\Bbb{R}-\left\lbrace 0 \right\rbrace$ si verifica una situazione paradossale; la funzione infatti risulta continua per ogni $x$ reale; infatti per quanto piccolo sia $x$:

$ Segno(x \pm ε) - Segno(x) = 1 - 1 = 0 \quad per \quad x>0\\Segno(x \pm ε) - Segno(x) = -1 + 1 = 0 \quad per \quad x \lt 0 $

Dunque la funzione risulta continua in tutto il suo dominio, pur presentando un salto ed essendo quindi discontinua dal punto di vista intuitivo. Però la funzione non risulta uniformemente continua; infatti se prendiamo come dominio $\Bbb{R}^{*}-\left\lbrace 0 \right\rbrace$ e due suoi valori infinitesimi positivi $\delta$ e $\epsilon$ si ha $ Segno(ε) - Segno(δ) = 1 - 1 = 0$ e quindi continuità; ma se si prendono $\delta$ e $\epsilon$ di segno opposto, per esempio $\delta \lt 0$ si ha:

$ Segno(δ) - Segno(ε) = -1 - (1) = -2$ e la funzione presenta un salto.

Insomma nella monade di zero c'è un salto e in questo senso il concetto di continuità uniforme è forse più vicino a quello intuitivo di continuità; vedi anche l'esempio successivo.

• La funzione $y = \frac{1}{x}$ (vedi iperbole equilatera) è continua in qualsiasi punto del dominio $\mathbb{R} - \{0\}$ cioè per $x \ne 0$; infatti $ f(x+\epsilon)-f(x) = \frac{1}{x+\epsilon} - \frac{1}{x} = \frac{x+\epsilon - x}{x(x+\epsilon)} = \frac{\epsilon}{x(x+\epsilon)}$ e quindi a incremento infinitesimo della $x$ corrisponde incremento infinitesimo della $y$. Questo risultato appare in contrasto con l'intuizione visto che al centro della curva c'è un visibilissimo salto, un salto infinito.
• Continuità uniforme: tutto come prima, ma non se $x_1$ e $x_2$ sono entrambi infinitesimi, per esempio $x_1 = \epsilon$ e $x_2 = 2\epsilon$ e quindi: $ f(\epsilon)-f(2\epsilon) = \frac{1}{\epsilon} - \frac{1}{2\epsilon} = \frac{2\epsilon-\epsilon}{2\epsilon} = \frac{\epsilon}{2\epsilon} = \frac{1}{2}$ e si ha quindi un salto finito, una discontinuità; lo stesso se si prendono due infinitesimi di segno opposto $x_1 = \epsilon$ e $x_2 = -\epsilon$ (verifica per esercizio: salto infinito!); quindi l'iperbole non è uniformemente continua, ha salti finiti e infiniti nella monade di centro 0 e questo corrisponde meglio all'intuizione.