

Le funzioni floor e ceil (dall'inglese floor = pavimento e ceiling = soffitto) sono due funzioni che convertono un qualsiasi numero razionale, reale o iperreale in un numero intero secondo le regole definite qui sotto; vengono indicate anche con mezze parentesi quadre che danno intuitivamente l'idea del pavimento e del soffitto.
|
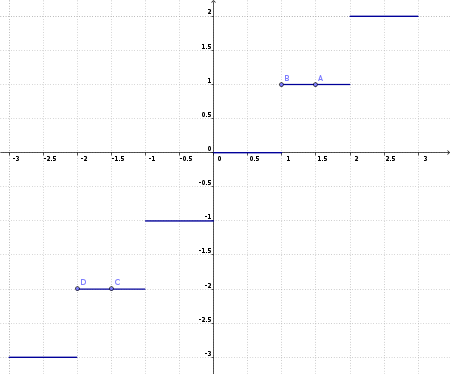
Funzione $floor(x) = \lfloor x \rfloor$: restituisce il numero intero immediatamente inferiore o uguale ad x, come negli esempi nella tabella a destra. Verifichiamo che la funzione è continua sia a destra, sia a sinistra per $x=1.5$ (*): $ f(x+\epsilon)-f(x) = \lfloor{1.5+\epsilon}\rfloor-\lfloor{1.5}\rfloor = 1 - 1 = 0 $ Verifichiamo che la funzione è continua a destra per $x=1$: $ f(x+\epsilon)-f(x) = \lfloor{1+\epsilon}\rfloor-\lfloor{1}\rfloor = 1 - 1 = 0 $ ma non a sinistra: $ f(x-\epsilon)-f(x) = \lfloor{1-\epsilon}\rfloor-\lfloor{1}\rfloor = 0 - 1 = -1 $ Questo risultato fornisce una misura del salto che la funzione fa andando verso sinistra. In modo del tutto analogo si verifica la continuità o discontinuità in altri punti. | $ \begin{array}{l | l} \lfloor{1.5}\rfloor = 1\\ \lfloor{1}\rfloor = 1\\ \lfloor{0.99}\rfloor = 0 \\ \lfloor{-0.99}\rfloor = -1 \\ \lfloor{-1}\rfloor = -1 \\ \lfloor{-1.5}\rfloor = -2 \\ \end{array} $ |
|
|
Funzione $ceil(x) = \lceil x \rceil $: restituisce il numero intero immediatamente superiore o uguale ad x, come negli esempi nella tabella a destra. Verifichiamo che la funzione è continua sia a destra, sia a sinistra per $x=1.5$(*): $ f(x+\epsilon)-f(x) = \lceil{1.5+\epsilon}\rceil - \lceil{1.5}\rceil = 2 - 2 = 0 $ Verifichiamo che la funzione è discontinua a destra per $x=1$: $ f(x+\epsilon)-f(x) = \lceil{1+\epsilon}\rceil - \lceil{1}\rceil = 2 - 1 = 1 $ anche questo risultato fornisce una misura del salto che la funzione fa andando verso destra; la funzione è invece continua a sinistra: $ f(x-\epsilon)-f(x) = \lceil{1-\epsilon}\rceil - \lceil{1}\rceil = 1 - 1 = 0 $ In modo del tutto analogo si verifica la continuità o discontinuità in altri punti. | $ \begin{array}{l | l} \lceil{1.5}\rceil = 2\\ \lceil{1}\rceil = 1\\ \lceil{0.999}\rceil = 1 \\ \lceil{-0.999}\rceil = 0 \\ \lceil{-1}\rceil = -1 \\ \lceil{-1.5}\rceil = -1 \end{array} $ |

|