Studiare la funzione: $ y = \frac{x^3}{x^2-4}$

Si tratta di una curva algebrica di 3º grado (cubica), infatti mettendola in forma implicita si ha

$ x^2{y} - 4y = x^3 \quad ovvero \quad x^2{y} - x^3 - 4y = 0 $

che è appunto di 3º grado.

Vediamo i singoli passi dello studio

1. Insieme di definizione è $ R - \{-2, +2 \} $ dovendo essere il denominatore $ x^2 - 4 = (x - 2)(x + 2) \ne 0 $.
2. Ricerca di eventuali asintoti verticali

   Per $ x = -2 , x = + 2 $ ci possono essere asintoti verticali; verifichiamolo per x = - 2 calcolando il valore della funzione per $ x = -2+ε \quad o \quad x = -2-ε $:

   $ \require{cancel} y = f(-2+ε) = \frac{(-2+ε)^3}{(-2+ε)^2-4} = \frac{-8 +12ε - 6ε^2 + ε^3}{\cancel{4}-2ε+ε^2-\cancel{4}} = \frac{-8 +12ε - 6ε^2 + ε^3}{-2ε+ε^2} = 4ω + ... = +\infty \left( = \lim\limits_{x \to -2^{+}}\frac{x^3}{x^2-4} \right) \\ y = f(-2-ε) = \frac{(-2-ε)^3}{(-2-ε)^2-4} = \frac{-8 -12ε - 6ε^2 - ε^3}{\cancel{4}+2ε+ε^2-\cancel{4}} = \frac{-8 -12ε - 6ε^2 - ε^3}{2ε+ε^2} = -4ω + ... = -\infty \left( = \lim\limits_{x \to -2^{-}}\frac{x^3}{x^2-4} \right) $

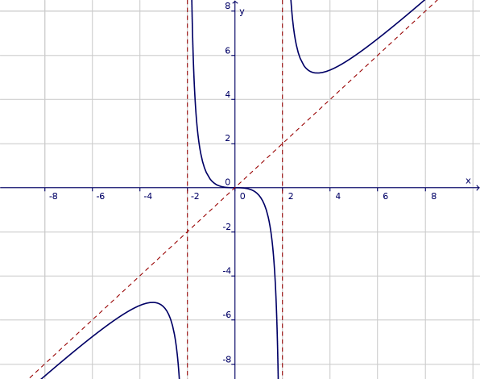
   Analogamente per $ x = +2+ε \quad o \quad x = +2-ε $. Ci sono quindi due asintoti verticali: $ x = -2 $ e $ x = +2 $.

3. Ricerca di eventuali asintoti obliqui.

   Il polinomio al numeratore ha grado superiore a quello del denominatore, dunque può esserci un asintoto obliquo, come si verifica calcolando i limiti:

   $ \require{cancel} m = \frac{f(ω)}{ω} = \frac{ω^3}{ω(ω^2-4)} = \frac{ω^3}{ω^3-4ω} = 1 + 4ε^2 + ... \simeq 1 \left( = \lim\limits_{x \to \infty}\frac{x^3}{x(x^2-4)} \right) \\ m = \frac{f(-ω)}{-ω} = \frac{-ω^3}{-ω(ω^2-4)} = \frac{-ω^3}{-ω^3+4ω} = 1 - 4ε^2 + ... \simeq 1 \left( = \lim\limits_{x \to \infty}\frac{x^3}{x(x^2-4)} \right) \\ q = f(ω) - m{ω} = \frac{ω^3}{ω^2-4} - mω = \frac{\cancel{ω^3} - \cancel{ω^3} + 4ω}{ω^2-4} = \frac{4ω}{ω^2-4} = 4ε + ... \simeq 0 \left( = \lim\limits_{x \to \infty}{\frac{x^3}{x^2-4} - mx} \right) $

   C'è quindi un asintoto obliquo $ y = x $.

4. Ricerca degli zeri della funzione, ovvero soluzione dell'equazione f(x) = 0.

   La frazione è uguale a 0 se e solo se lo è il numeratore, dunque l'equazione si riduce a

   $ x^3 = 0 \quad → x = 0 $

   Vi è dunque un solo zero nell'origine.

5. Studio del segno della funzione, (soluzione della disequazione $ f(x) > 0 $).

   Qui occorre considerare anche il segno del denominatore e considerare il segno dei tre fattori $ x, (x - 2), (x + 2) $ e riassumere con il solito schema

   $ \begin{array}{lccccc} \\ & &-2& &0& &+2& \\ x > -2 &-----&o&+++++&+&+++++&+&+++++ \\ x > 0 &-----&+&-----&o&+++++&+&+++++ \\ x > +2 &-----&-&-----&-&-----&o&+++++ \\ & - &o& + &o& - &o& + \end{array}$

   La funzione è positiva per (-2 < x < 0) v (x > 2)

6. Ricerca dei massimi, dei minimi e dei flessi.

   Calcoliamo la derivata:

   $ y' = \frac{3x^2(x^2-4)-{x^3}{2x}}{(x^2-4)^2} = \frac{3x^4-12x^2-2x^4}{(x^2-4)^2} = \frac{x^4-12x^2}{(x^2-4)^2} = \frac{x^2(x^2-12)}{(x^2-4)^2} $

   La derivata si annulla quando si annulla il numeratore $ x^2(x^2 - 12) = 0 $. Le soluzioni sono tre: $ x = -2\sqrt{3}, x = 0, x = +2\sqrt{3} $. (essendo $ \sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3}$). Lo studio del segno della derivata è:

   $ \begin{array}{lccccc} \\ & &-2\sqrt{3}& &0& &+2\sqrt{3}& \\ x > -2\sqrt{3} &-----&o&+++++&+&+++++&+&+++++ \\ x^2 > 0 &+++++&+&+++++&o&+++++&+&+++++ \\ x > +2\sqrt{3} &-----&-&-----&-&-----&o&+++++ \\ & + &o& - &o& - &o& + \\ & ↗ &→& ↘ &→& ↘ &→& ↗ \end{array}$

   Ne segue che:

   • Per x = −2√3 c'è un massimo: $ Max(-2\sqrt{3}; -\sqrt{27}) \approx Max(-3,46; -5,20)$.
   • Per x = 0 c'è un flesso a tangente orizzontale decrescente $ Flex(0;0) $.
   • Per x = +2√3 c'è un minimo: $ Min(2\sqrt{3}; \sqrt{27}) \approx Min(+3,46; +5,20)$.

In definitiva il grafico della funzione è quello riportato a lato.