

La ricerca degli asintoti obliqui è analoga a quella degli asintoti orizzontali. Si possono seguire due metodi:
| Metodo infinitesimale | Eq. asintoto $y = mx + q$ | $m = st \left(\frac{f(\omega)}{\omega} \right)\\q = st \left(f(\omega)-m\omega \right)$ | (valido per qualsiasi funzione $y = f(x)$): calcolare la parte standard di $ \frac{f(\omega)}{\omega} $ se è un numero limitato $m$, questo è il coefficiente angolare dell'asintoto. Calcolando poi $ f(\omega) - m\omega $ la sua parte standard sarà il termine noto q, e l'asintoto obliquo avrà quindi equazione $ y = mx + q $. |
|---|---|---|---|
| Solo se $m$ è un numero limitato (non infinito) | |||
| Metodo algebrico | Metodo valido solo per funzioni algebriche fratte tipo: $f(x) = \frac{P(x)}{Q(x)}$ | Dividere i due polinomi con la regola di Ruffini; il quoziente, se è un polinomio di 1° grado, ci dà l'equazione dell'asintoto obliquo. Di norma c'è asintoto obliquo se $Q(x)$ ha grado $n$ e $P(x)$ grado $n+1$ e se il resto non è zero, altrimenti la curva degenera in una retta. | |
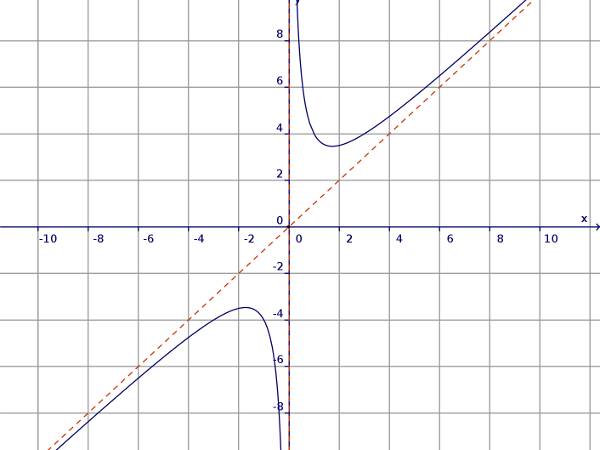
Cercare l'eventuale asintoto obliquo di
$$ y = \frac{x^2+3}{x} $$
Per la divisione basta applicare la proprietà distributiva della divisione:
$ \frac{x^2+3}{x} = x + \frac{3}{x} $
e l'asintoto obliquo è $y = x$ (bisettrice del primo quadrante).
$ f(\omega) =\frac{\omega^2 + 3}{\omega} = \omega + 3\epsilon = \infty$(*)
$\frac{f(\omega)}{\omega} =\frac{\omega^2 + 3}{\omega^2} = 1 + 3\epsilon^2 \simeq 1 $ (*)
Dunque il coefficiente angolare dell'asintoto è $ m = 1 $. Si noti che nel risultato $ 1 + 3\epsilon^2 $ è significativa anche la parte infinitesima: il fatto che sia positiva ci dice che la curva sta sopra l'asintoto, per numeri molto grandi positivi. Per numeri grandi negativi basta calcolare $ \frac{f(-\omega)}{-\omega} $
$ \frac{f(-\omega)}{-\omega} =\frac{-\omega^2 + 3}{-\omega^2} = 1 - 3\epsilon^2 \simeq 1 $
e in questo caso la parte infinitesima di $1 - 3\epsilon^2$ significa che la curva sta sotto l'asintoto. Calcoliamo ora il termine noto $q$:
$ \frac{\omega^2 + 3}{\omega} - \omega = \frac{\omega^2 + 3 - \omega^2}{\omega} = \frac{3}{\omega} = 3\epsilon \simeq 0 $ (*)
e quindi è q = 0; l'asintoto obliquo è $ y = x $.
_(x-1).png)
Cercare l'eventuale asintoto obliquo di
$$ y = \frac{2x^2+1}{x-1} $$
2x2 + ... - 1 | x - 1
-2x2 + 2x |-------
---------------| 2x + 2
+ 2x - 1 |
- 2x - 2 |
dunque la funzione può scriversi come $x + \frac{3}{x} $, e l'asintoto obliquo è $ y = 2x + 2 $.
$ \require{cancel} \frac{2\omega^2 + 1}{\omega(\omega-1)} = \frac{\cancel{\omega^2}(2 + \epsilon^2)}{\cancel{\omega^2}(1-\epsilon)} \simeq 2\quad$ (*)
Dunque è m = 2. Calcoliamo ora:
$ \require{cancel} \frac{2\omega^2 + 1}{\omega-1} - 2\omega = \frac{\cancel{2\omega^2} + 1 - \cancel{2\omega^2} + 2\omega}{\omega-1} \simeq 2 $
e quindi è q = 2; l'asintoto obliquo è $ y = 2x + 2 $.