Data una funzione $ y = f(x) $, si dice asintoto orizzontale una retta parallela all'asse delle x, con la quale la funzione ha in comune il punto all'infinito.

In modo più rigoroso, si dice che una funzione ha un asintoto orizzontale quando(*) il suo valore per $x$ infinitamente grande è un numero infinitamente vicino a un numero finito, e cioè:

$ f(ω) \simeq k $ o che è lo stesso $ f(ω) = k + ε$ o $ f(ω) = k - ε$

e l'asintoto è la retta orizzontale $y=k$.

In particolare se $ f(ω) \simeq 0 $ l'asintoto orizzontale è l'asse delle x ($ y = 0 $). Questo avviene p.es. per l'iperbole equilatera $y = \frac{1}{x}$.

• Metodo degli iperreali (o dei limiti) (valido per qualsiasi funzione $y = f(x)$): calcolare $f(\omega)$; se ha una parte standard $k$, allora c'è un asintoto orizzontale con equazione $y = k$. (Analisi classica; calcolare il limite per $x → \pm\infty $)
• Metodo della divisione dei polinomi (algebrico) (solo se si tratta di una frazione algebrica):
  • Dividere i due polinomi con la consueta regola; se il quoziente è una costante $k$, allora c'è un asintoto orizzontale con equazione $y = k$.
  • Divisione degli iperreali: variante della precedente avendo posto $+ω$ al posto di $x$; se il quoziente è un numero iperreale limitato $ k \pm nε $, allora c'è un asintoto orizzontale con equazione $y = k$; il segno della parte infinitesima ci dice se la curva si avvicina all'asintoto da sopra o da sotto per $ x \to +\infty$. Ponendo $-ω$ al posto di x si ha il comportamento per $ x \to -\infty$.

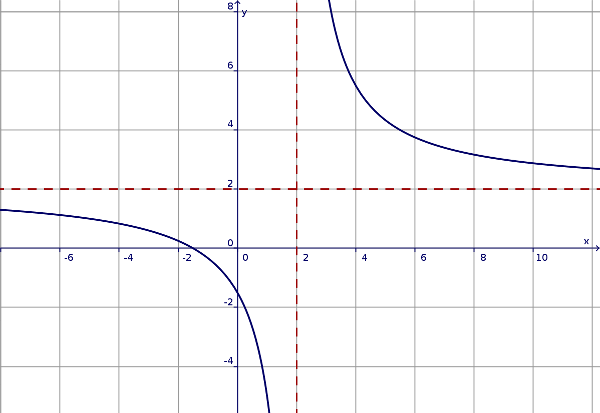
Cercare l'eventuale asintoto orizzontale di

$$ y = \frac{2x + 3}{x - 2} $$

• Metodo degli iperreali. Calcoliamo:

  $$ \require{cancel} st \left(\frac{2ω + 3}{ω - 2} \right) = st \left(\frac{\cancel{ω}(2 + 3ε)}{\cancel{ω}(1 - 2ε)} \right) = 2 $$

  che conferma l'asintoto orizzontale $ y = 2 $ tratteggiato in rosso nel disegno a lato.(*)

• Metodo algebrico. Eseguendo la divisione si ha

  $ \begin{array}{l | l } \quad 2x + 3 & x - 2 \\ -2x + 4 &―――――― \\ ―――――& 2 \\ \quad \quad \quad + 7 & \end{array} $

  dunque la funzione può scriversi come $ 2 + \frac{7}{x -2} $, e l'asintoto orizzontale è $ y = 2 $ (vedi figura a lato).
• Divisione tra numeri infinitamente grandi

  $ \begin{array}{l | l } \quad 2ω + 3 & ω - 2 \\ -2ω + 4 &―――――― \\ ―――――& 2 + 7ε \\ \quad \quad \quad + 7 & \end{array} $

  Il risultato $ 2 + 7ε $ ovviamente conferma l'asintoto orizzontale $ y = 2 $ ma fornisce in più l'informazione che la curva si avvicina all'asintoto da sopra per $ x \to \infty$; calcolando per x = -ω si ha invece:

  $ \begin{array}{l | l } -2ω + 3 &-ω - 2 \\ +2ω + 4 &―――――― \\ ―――――& 2 - 7ε \\ \quad \quad \quad + 7 & \end{array} $

  che ci dice che la curva si avvicina all'asintoto da sotto per $ x \to -\infty$.

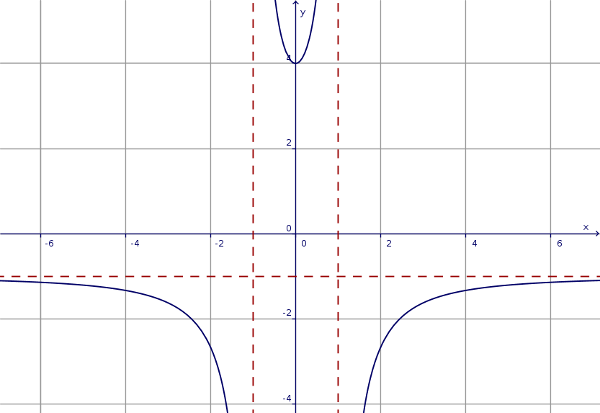
Cercare l'eventuale asintoto orizzontale di

$$ y = \frac{x^2 + 4}{1 - x^2} $$

• Metodo degli iperreali. Calcoliamo:

  $$ \require{cancel} st \left(\frac{ω^2 + 4}{1 - ω^2} \right) = st \left(\frac{\cancel{ω^2}(1 + 4ε^2)}{\cancel{ω^2}(ε^2 -1)} \right) = -1$$

  che conferma l'asintoto orizzontale $ y = -1 $ (*).
• Metodo algebrico.

  Eseguendo la divisione si ha:

  $ \begin{array}{l | l } \quad x^2 \quad + 4 & -x^2 + 1 \\ -x^2 \quad + 1 &―――――― \\ ―――――& -1 \\ \quad \quad \quad + 5 & \end{array} $

  dunque la funzione può scriversi come $ -1 + \frac{5}{1 - x^2} $, e l'asintoto orizzontale è $ y = -1 $ (vedi figura a lato).