Data una funzione $ f(x) $ si dice asintoto verticale una retta verticale $ x = a $, dove $a$ è un valore per il quale la funzione non è definita, alla quale la funzione è infinitamente vicina (si avvicina illimitatamente senza mai toccarla). In altri termini la funzione cresce illimitatamente all'avvicinarsi alla retta.

La funzione ovviamente può avvicinarsi all'asintoto da destra (da valori maggiori di $a$) o da sinistra (da valori minori di $a$). Nei casi più semplici come l'iperbole equilatera la cosa avviene da entrambe le parti.

Formalizzando la ricerca degli asintoti si riduce a (il simbolo $\infty$ è qui usato nel senso di un numero infinitamente grande qualsiasi):

1. individuare i valori $x_i$ di possibile asintoto, di norma quelli per i quali non è definita, tipicamente per denominatore uguale a zero;
2. calcolare la funzione per $x_i+ε$ (da destra) ed $x_i-ε$ (da sinistra). Se il risultato è un numero infinitamente grande c'è un asintoto verticale $x = x_i$; se invece si ottiene un valore finito allora siamo in presenza di una discontinuità eliminabile.
3. Se è $ f(x_0 + ε) = \pm\infty $ la curva tende a $ \pm\infty$ da destra.
4. Se è $ f(x_0 - ε) = \pm\infty $ la curva tende a $ \pm\infty$ da sinistra.
5. Se la curva tende a $+\infty$ da destra e a $-\infty$ da sinistra, o viceversa l'asintoto si dice semplice.
6. Se la curva tende a $+\infty$ (o a $-\infty$) sia da destra sia da sinistra l'asintoto si dice doppio.

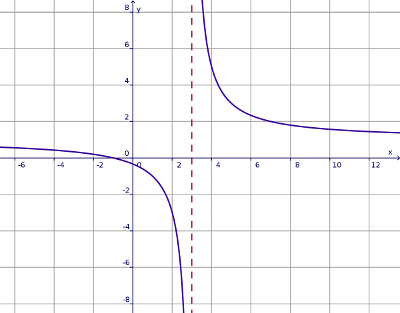
$$ y = \frac{x+1}{x-3} $$

Per $ x = 3 $ la funzione non è definita (il denominatore $ x - 3 $ si annulla); il dominio è R - {3}; potrebbe quindi esserci un asintoto verticale; per verificarlo calcoliamo la funzione per $ x = 3 + ε $:

$ y = \frac{3 + ε + 1 }{3 + ε - 3} = \frac{4 + ε}{ε} = 4ω + 1 = +\infty$ (*)

e per $ x = 3 - ε $:

$ y = \frac{3 - ε + 1 }{3 - ε - 3} = \frac{4 - ε}{-ε} = -4ω + 1 = -\infty$ (*)

dunque la funzione tende a infinito positivo da destra e a infinito negativo da sinistra; c'è un asintoto verticale semplice $x=3$; vedi figura a lato.

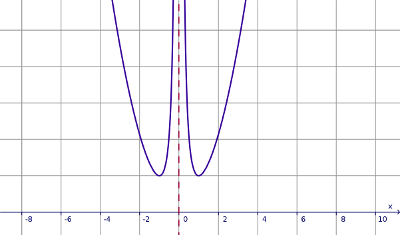
$$ y = f(x) = x^2 + \frac{1}{x^2} $$

Per x = 0 la funzione non è definita; potrebbe quindi esserci un asintoto verticale; per verificarlo calcoliamo la funzione per $ x = 0 + ε = ε $:

$ f(ε) = ε^2 + \frac{1}{ε^2} = ε^2 + ω^2 = +\infty$ (*)

e analogamente per $ x = 0 - ε = -ε $:

$ f(-ε) = (-ε)^2 + \frac{1}{(-ε)^2} = ε^2 + ω^2 = +\infty $

dunque la funzione vale +ω a destra e a sinistra; c'è un asintoto verticale doppio $x=0$; vedi figura a lato.

$$ y = f(x) = \frac{x^2-1}{x+1} $$

Per $ x = -1 $ la funzione non è definita, il dominio è R -{-1}; potrebbe quindi esserci un asintoto verticale; per verificarlo calcoliamo la funzione per $ x = -1 \pm ε $

$ f(-1 \pm ε) = y = \frac{(-1 \pm ε)^2-1}{-1 \pm ε+1} = \frac{1 \mp 2ε + ε^2 -1}{\pmε} = \frac{\mp 2ε + ε^2}{\pm ε} = -2 \pm ε \simeq -2$(*)

dunque la funzione in questo caso non va affatto a infinito per x = -1 ma è infinitamente vicina a -2 (ovvero tende a 2); questo vuol dire che può essere completata ponendo $f(-1) = -2$. In effetti si tratta di una frazione algebrica semplificabile, dal momento che $ x^2 - 1 = (x - 1)(x + 1) $; la funzione semplificata vale $ y = x - 1 $, che per $x = -1$ vale appunto -2. Una discontinuità di questo tipo si dice eliminabile.