Grafico della funzione

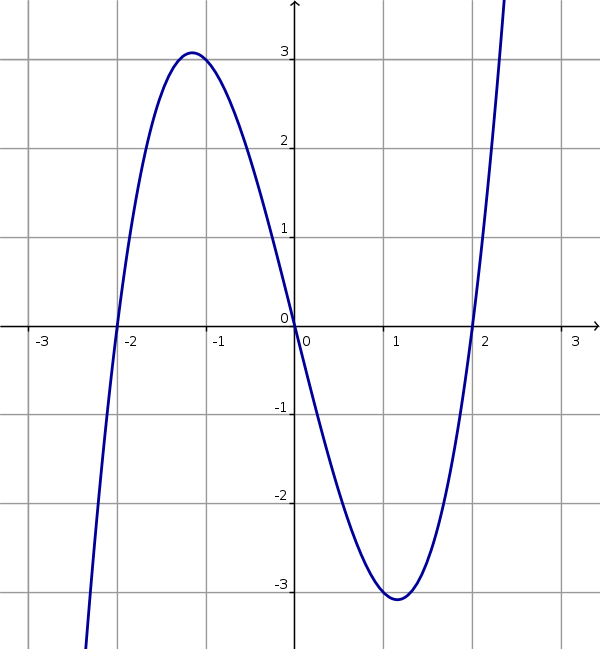
Studiare la funzione

$$y = x^3 - 4x$$

Si tratta di una curva algebrica di 3º grado (cubica)

Vediamo i singoli passi dello studio

1. Insieme di definizione: si tratta di un polinomio calcolabile per ogni numero reale, dunque $D = R$.
2. Ricerca di eventuali asintoti: i polinomi non hanno asintoti.
3. Ricerca degli zeri della funzione, ovvero soluzione dell'equazione x³ - 4x = 0. Basta mettere in evidenza x e quindi fattorizzare la differenza di quadrati: $ x(x^2 - 4) = 0 ; x(x - 2)(x + 2) = 0$
   Vi sono quindi tre zeri: $x = -2; x = 0; x = +2.$
4. Studio del segno della funzione, ovvero soluzione della disequazione $x^3 - 4x = 0$. Utilizzando il risultato appena ottenuto la disequazione si spezza in tre disequazioni elementari:

                            -2       0       +2
   x + 2 > 0    -------------o+++++++++++++++++++++++++++++
   x > 0        ---------------------o+++++++++++++++++++++
   x - 2 > 0    ------------------------------o++++++++++++
                     -          +         -        +
   

   La funzione è negativa per x < -2 e 0 < x < 2 e positiva altrove.
5. Calcolo delle derivate La derivata si ottiene utilizzando la regola di derivazione del polinomio: $$y' = 3x^2 - 4$$ Le derivate successive sono: $ \\f''(x) = 6x \\f'''(x) = 6 $
6. Ricerca dei massimi, dei minimi e dei flessi.

   Si tratta di risolvere l'equazione f'(x) = 0, in questo caso $3x^2 - 4 = 0 \rightarrow x^2 = \frac{4}{3}$ che ha per soluzioni: $ x = \pm \sqrt{\frac{4}{3}} $. Si hanno quindi due punti stazionari per $x= -\frac{2}{\sqrt{3}}$ e $x= +\frac{2}{\sqrt{3}}$ usando il II metodo si calcola la derivata seconda $f''(x)=6x$ per ogni punto:

   $\begin{matrix} I & x= -\frac{2}{\sqrt{3}} & f"(-\frac{2}{\sqrt{3}}) = 6 \times (-\frac{2}{\sqrt{3}}) = -\frac{12}{\sqrt{3}} < 0 & massimo \\II & x= +\frac{2}{\sqrt{3}} & f"(+\frac{2}{\sqrt{3}}) = 6 \times \frac{2}{\sqrt{3}} = \frac{12}{\sqrt{3}} > 0 & minimo \end{matrix}$

   Le ordinate dei due punti si ottengono sostituendo nell'equazione di partenza $y = x^3-4x$.

   $\begin{matrix} I & x= -\frac{2}{\sqrt{3}} & f(-\frac{2}{\sqrt{3}}) = -\frac{8}{\sqrt{27}} + \frac{8}{\sqrt{3}} = -\frac{8-24}{3\sqrt{3}} = \frac{16}{3\sqrt{3}} \approx 3,079 \\II & x = \frac{2}{\sqrt{3}} & f(-\frac{2}{\sqrt{3}}) = \frac{8}{\sqrt{27}} - \frac{8}{\sqrt{3}} = \frac{8-24}{3\sqrt{3}} = -\frac{16}{3\sqrt{3}} \approx -3,079 \end{matrix}$

   e in definitiva si hanno i due punti stazionari:

   $\begin{matrix} Max (-\frac{2}{\sqrt{3}}; +\frac{16}{3\sqrt{3}}) \approx (-1,15; +3,08) \\Min (+\frac{2}{\sqrt{3}}; -\frac{16}{3\sqrt{3}}) \approx (+1,15; -3,08) \end{matrix}$

   Riassumendo tutti questi risultati si ottiene il grafico riportato sopra.