Il metodo si basa sulla regola di Fermat relativa ai punti stazionari (massimi, minimi, flessi a tangente orizzontale) la tangente è orizzontale, e quindi la derivata deve essere nulla.

Si tratta quindi, prima di tutto, di calcolare la derivata $f'(x)$ e porre $f'(x) = 0$.

Se siamo capaci di risolvere l'equazione $f'(x) = 0$ e calcolare le sue soluzioni $x_0, x_1, x_2 \dots $ queste saranno le ascisse dei punti stazionari.

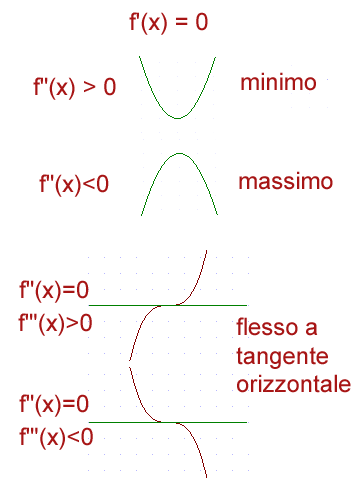
Ognuno di questi punti può essere un massimo, un minimo o un flesso a tangente orizzontale; per decidere quale sia il caso, si studiano le derivate successive, prima di tutte la derivata seconda, che ha il significato geometrico di concavità (o convessità).

Si calcola quindi la derivata seconda $y" = f"(x)$ che è comunque una funzione della $x$; si sostituisce la $x$ con il valore del sospetto massimo o minimo e si controlla il segno.

[N.B. qui della derivata seconda ci interessa solo il segno; se questo è evidente fin dall'inizio è inutile sobbarcarsi al calcolo esatto del suo valore]

A questo punto sono possibili tre casi

1. la derivata seconda è positiva, la concavità è verso l'alto e abbiamo un minimo.
2. la derivata seconda è negativa, la concavità è verso il basso e abbiamo un massimo.
3. la derivata seconda è nulla (caso dubbio) in questo caso non si può concludere nulla, ma occorre calcolare le derivate successive secondo il seguente schema
1. se la prima derivata che non si annulla è di ordine dispari, c'è un flesso a tangente orizzontale (crescente o decrescente secondo che la derivata è positiva o negativa).
2. se la prima derivata che non si annulla è di ordine pari, c'è un massimo o un minimo; il segno di questa derivata ha lo stesso significato della derivata seconda se è positivo si ha un minimo; se è negativo si ha un massimo.

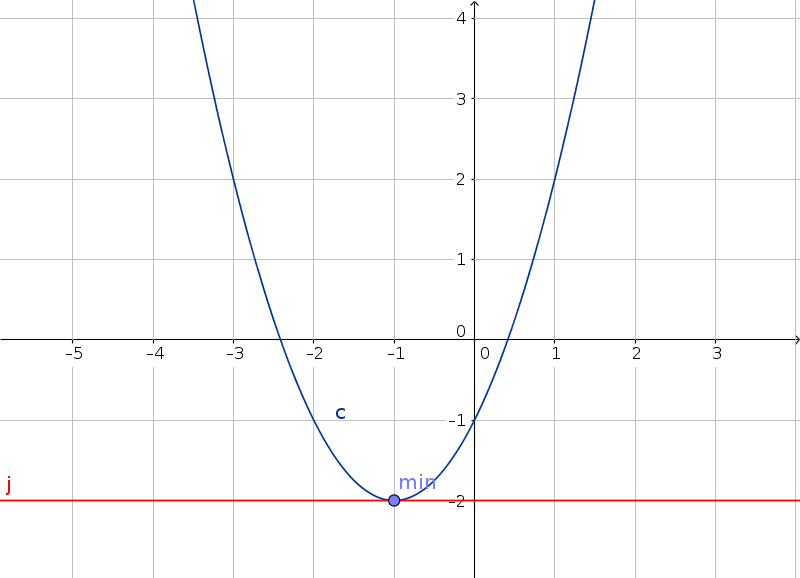
Sia data la funzione $y = x^2 + 2x - 1$ (si tratta di una normalissima parabola).

La derivata è $y' = 2x + 2$

Uguagliando a zero si ha l'equazione $2x + 2 = 0$, e quindi $2x = -2$ e $x = -1$.

Dunque per $x = -1$ si ha un possibile massimo o minimo.

Per decidere si calcola la derivata seconda $f''(x) = 2$ che per $x = -1$ (in verità per qualsiasi $x$) è positiva, dunque ha un minimo con $x=-1$, che è poi il vertice della parabola.

La $y$ del minimo si trova sostituendo nell'equazione della primitiva

$y = x^2 + 2x - 1 = (-1)^2 + 2*(-1) - 1 = +1 - 2 - 1 = - 2$.

Dunque abbiamo un punto di minimo $min(-1, -2)$ che è poi il vertice della parabola.

Clic sulla freccia per vedere il grafico della funzione nelle vicinanze dell'origine: (→).

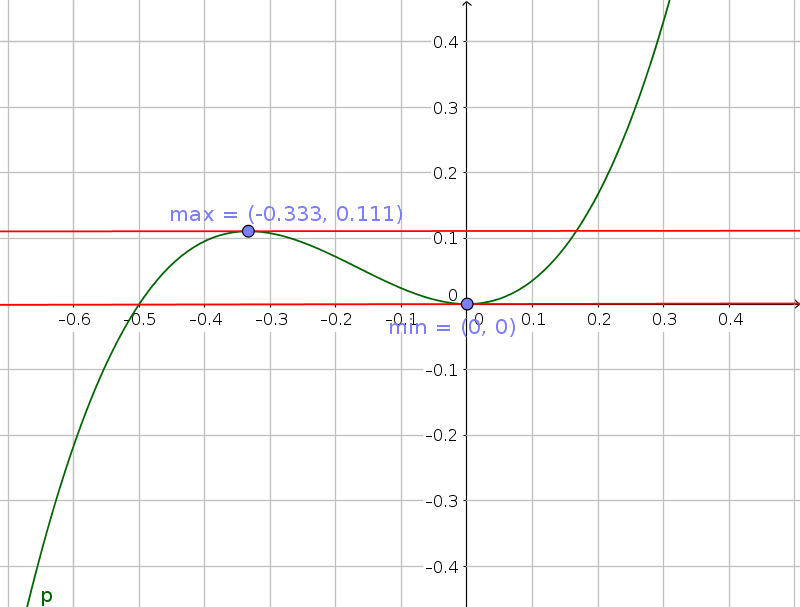
Sia data la funzione $y = 6x^3 + 3x^2$ (parabola cubica).

La derivata è $y' = 18x^2 + 6x$

Uguagliando a zero si ha l'equazione $18x^2 + 6x = 0$, e quindi mettendo in evidenza $6x(3x + 1) = 0$; dunque si hanno le due soluzioni

1. $6x = 0; x = 0$
2. $3x + 1 = 0; x = -\frac{1}{3}$

Dunque abbiamo due possibili punti di massimo o minimo.

Per decidere si calcola la derivata seconda $y" = 36x + 6$.

1. I caso per $x = -\frac{1}{3}$ si ha $y'' = 36(-\frac{1}{3}) + 6 = -12 + 6 = -6 < 0$; si tratta di un massimo.
2. II caso per $x = 0$ si ha $y" = 6 = +6 > 0$ e dunque c'è un minimo.

La $y$ dei due punti si trova sostituendo nell'equazione della primitiva:

1. $x = -\frac{1}{3} y = 6(-\frac{1}{27}) + 3(\frac{1}{9}) = -\frac{6}{27} + \frac{3}{9} = -\frac{2}{9} + \frac{3}{9} = \frac{1}{9} = 0.1111 \dots$.
2. $x = 0; y = 6 \times 0 + 3 \times 0 = 0$.

In definitiva abbiamo:

• un massimo $max \left( -\frac{1}{3}, \frac{1}{9} \right)$.
• un minimo $min (0, 0)$.

Clic sulla freccia per vedere il grafico della funzione nelle vicinanze dell'origine: (→).

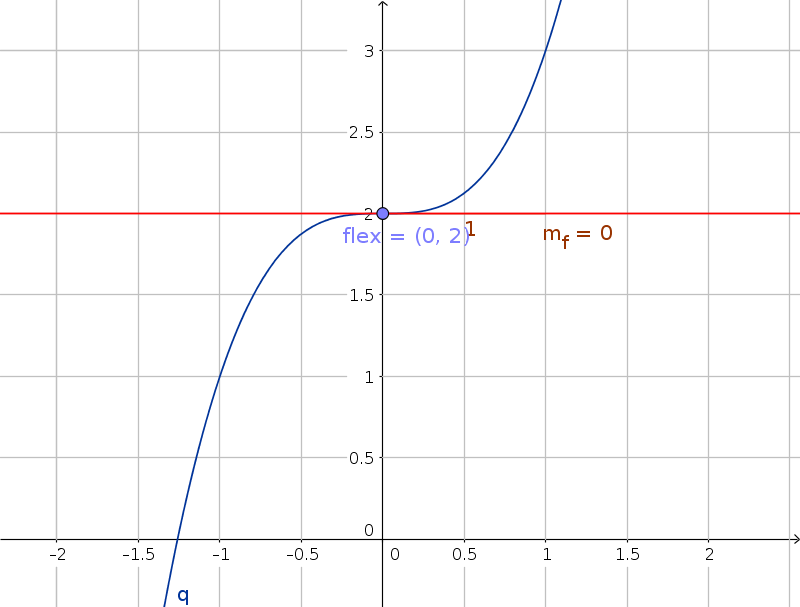
Sia data la funzione $y = x^3 + 2$ (parabola cubica).

La derivata è $y' = 3x^2$;

Uguagliando a zero si ha l'equazione $3x^2 = 0$, e quindi si ha una sola soluzione $x = 0$;

Per decidere si calcola la derivata seconda $y" = 6x$ che per $x = 0$ si annulla a sua volta; siamo quindi nel caso dubbio.

Si calcola allora la derivata terza $y''' = 6$ che è comunque positiva; dunque la prima derivata che non si annulla è di ordine dispari, e si tratta di un flesso a tangente orizzontale.

Clic sulla freccia per vedere il grafico della funzione nelle vicinanze dell'origine: (→).

X

X

X