

|
L'analisi infinitesimale nasce da alcuni problemi che erano stati già messi in luce dal filosofo greco Zenone; le opere di Zenone sono andate perdute, ma Aristotele nelle sue opere ricorda questi quattro paradossi.
| |||||||||||
| Primo paradosso o della dicotomia |
Consideriamo un segmento di retta AB. Non è possibile percorrerlo per intero, infatti, partendo da A si dovrà prima toccare il punto C medio di AB, poi il punto D medio di CB, poi il punto E medio di DB e così via all'infinito.
Nel linguaggio matematico moderno possiamo tradurre così questo paradosso: la somma di infiniti termini $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+ ... +\frac{1}{2^n} + ... $ vale successivamente $\langle\frac{1}{2}, \frac{3}{4}, \frac{7}{8}, ... 1-\frac{1}{2^n} ... \rangle$ che è sempre minore di 1, anche se ci si avvicina sempre di più. Da questo problema nasce il concetto di limite e in modo equivalente di numero iperreale. 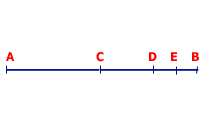
Secondo paradosso | Achille e la tartaruga
| Il pie' veloce Achille si trova nella posizione $A_0$ e deve raggiungere la tartaruga situata in $T_0$, molto più lenta; ma prima di raggiungere la tartaruga, Achille deve raggiungere la posizione $T_0$, e nel frattempo la tartaruga avrà raggiunto sia pur lentamente una nuova posizione $T_1$; a questo punto Achille deve raggiungere $T_1$, ma nel frattempo la tartaruga sarà arrivata in una nuova posizione $T_2$ e così via all'infinito. In conclusione il pie' veloce Achille non raggiungerà mai la tartaruga. Questo paradosso può essere considerato una variante dinamica del primo.
| Terzo paradosso | o della freccia
| Un arciere lancia una freccia. La freccia vola veloce, ma in un dato istante (tempo di durata nulla) si trova in una data posizione (spostamento nullo), e quindi è ferma in quella posizione. Paradossalmente il movimento risulta essere composto di posizioni ferme. Zenone concludeva che il movimento è una mera illusione. Nel linguaggio matematico moderno possiamo tradurre così questo paradosso: in un istante (intervallo di tempo di durata nulla $Δt = 0$) lo spostamento della freccia è nullo ($Δs = 0$). La velocità della freccia in quell'istante vale allora $\frac{Δs}{Δt} = \frac{0}{0}$ e quindi risulta indeterminata; non nulla come concludeva erroneamente Zenone ma comunque impossibile da calcolare e quindi il paradosso permane: non sembra possibile definire una velocità istantanea. Da questo paradosso nasce il calcolo infinitesimale che aggira l'ostacolo supponendo che istante di tempo non sia un tempo nullo ($Δt = 0$) ma un tempo infinitamente piccolo ($dt$) e analogamente si debba considerare uno spostamento infinitamente piccolo ($ds$); a questo punto la velocità istantatanea è semplicemente il quoziente di questi due numeri $\frac{ds}{dt}$. Nasce così il concetto di derivata.
| Quarto paradosso | o dello stadio
| Nella corsa delle bighe dell'antica Grecia le bighe correvano in uno stadio lungo un rettilineo fino a un pilone, ci giravano attorno e tornavano indietro. Capitava che la biga più veloce incrociasse la biga più lenta e la vedesse passare a velocità apparentemente superiore, cosa che a Zenone pareva impossibile. Più che di un paradosso si tratta di un effetto dovuto al fatto che le velocità non sono assolute ma relative al sistema di riferimento, concetto che probabilmente Zenone non aveva molto chiaro. Un effetto del tutto simile lo possiamo osservare viaggiando in treno quando incrociamo un altro treno; la velocità apparente è pari alla somma delle due velocità (assolute) rispetto alla terraferma. Questo paradosso è l'unico tra quelli di Zenone a non avere particolare interesse per il calcolo infinitesimale e lo riportiamo qui solo per completezza.
| | |
|---|---|---|---|---|---|---|---|---|---|---|---|