Un numero iperreale è rappresentato da una sequenza infinita di numeri reali, per esempio:

$ \omega = \left \langle 1, 2, 3, 4, 5 \ldots n \ldots\right \rangle$ (numero omega)
$ \epsilon = \left \langle 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5} \ldots 1/n \ldots \right \rangle = \frac{1}{\omega} \\ a = \left \langle 2, 2, 2, 2, 2, 2, 2, 2 \ldots \right \rangle = 2 \\ 2 + \epsilon = \left \langle 3, \frac{5}{2}, \frac{7}{3}, \frac{9}{4}, \frac{11}{5} \ldots \frac{2n + 1}{n} \ldots \right \rangle = \frac{2\omega + 1}{\omega} \simeq 2 $

Per maggiori dettagli si veda la pagina Iperreali in cifre

Un numero iperreale limitato è la somma di un numero reale (detto parte standard) e di un numero infinitesimo, p.es.:

$ 1 + {dx} $ (1 è la parte reale o standard, dx la parte infinitesima)

$ 2 + \epsilon \\ 2 + 2{dx} \\ x + y\epsilon $

I numeri iperreali infinitamente grandi o illimitati come $\omega$ non possono ovviamente essere scritti in questa forma.

I numeri iperreali possono dividersi in tre sottoinsiemi:

1. Numeri infinitesimi o infinitamente piccoli: numeri iperreali minori (in valore assoluto) di qualsiasi reale.
2. Numeri limitati: numeri iperreali che sono minori (in valore assoluto) di un qualche reale.
3. Numeri ilimitati o infinitamente grandi: numeri iperreali maggiori (in )valore assoluto) di qualsiasi reale.

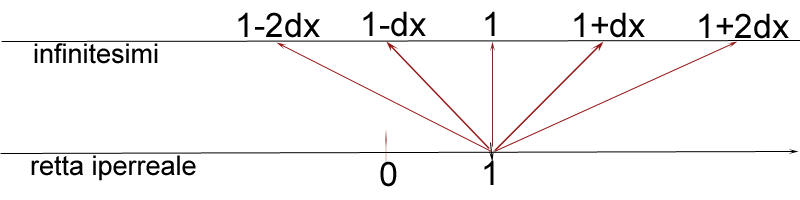
Per visualizzare gli iperreali si può immaginare che ogni numero della retta iperreale sia circondato da un microscopico intorno di infinitesimi, che in onore di Leibniz viene chiamato monade. Per esempio nel disegno a lato il numero 1 è circondato da infiniti numeri iperreali che hanno 1 come parte standard, p.es. 1-2dx, 1-dx, 1, 1+dx, 1+2dx; per mostrarli si è immaginato di usare un telescopio infinito (detto telescopio di Keisler) che espande l'intorno infinitesimo di 1 in una retta.

Il prodotto di un reale e un infinitesimo (p.es. 2dx) è un infinitesimo, il prodotto di due infinitesimi (p.es. $ {dx}^2 $) è un infinitesimo che possiamo chiamare del secondo ordine.(*)

Nella Analisi non standard ha importanza chiave la funzione st(z) (parte standard) che ad un qualsiasi numero iperreale z associa la sua parte reale.