Grafico della funzione Grafico allargato della funzione

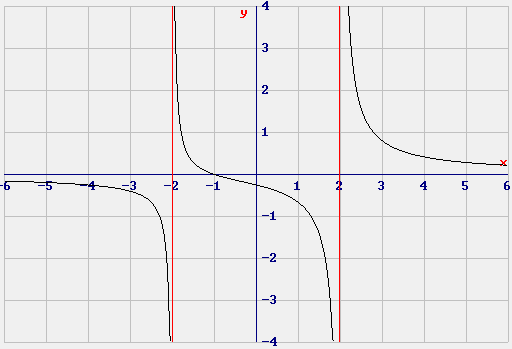
$$ y = \frac{x+1}{x^2-4} $$

Si tratta di una curva algebrica di 3° grado (cubica), infatti mettendola in forma implicita si ha

$ x^2{y} - 4y = x + 1 \quad ovvero \quad x^2{y} - x - 4y - 1 = 0 $

che è appunto di 3# grado.

Vediamo i singoli passi dello studio

1. Dominio (Insieme di definizione) è $\mathbb{R} - {-2, +2}$ dovendo essere il denominatore $ x^2 - 4 = (x - 2)(x + 2) \ne 0 $.
2. Ricerca di eventuali asintoti verticali per $x = -2$ e per $x = + 2$ ci possono essere asintoti verticali doppi; verifichiamolo calcolando la funzione per $ x = -2 - ε , x = -2 + ε $:

   $ \require{cancel} y = f(-2 - ε) = \frac{-2 - ε + 1}{(-2 - ε)^2 -4} = \frac{-1 - ε}{\cancel{4} + 4ε + ε^2 -\cancel{4}} = \frac{-1 - ε}{+4ε + ε^2} = -\frac{1}{4}ω + ... = -\infty \\ y = f(-2 + ε) = \frac{-2 + ε + 1}{(-2 + ε)^2 -4} = \frac{-1 + ε}{\cancel{4} - 4ε + ε^2 -\cancel{4}} = \frac{-1 + ε}{-4ε + ε^2} = +\frac{1}{4}ω + ... = +\infty $(*)

   e analogamente si trovano i valori per $ x = 2 - ε , x = 2 + ε $ ovverosia i limiti per x che tende a 2. In conclusione ci sono due asintoti verticali: $ x = -2, x = + 2 $

3. Ricerca di eventuali asintoti orizzontali od obliqui. Il polinomio al numeratore ha grado inferiore a quello del denominatore, dunque c'è un asintoto orizzontale y = 0 (l'asse delle x), come si verifica calcolando la funzione per $ x = \pm ω$

   $ y = f(-ω) = \frac{-ω + 1}{ω^2 -4} = \frac{-ω(1+ε}{ω^2(1 -4ε^2} = -ε(1 + ...) \simeq 0\\ \\ y = f(+ω) = \frac{+ω + 1}{ω^2 -4} = ε(1 + ...) \simeq 0 $ (*)

   In definitiva la cubica ha per asintoti l'asse delle $x$ e le due rette $x = \pm 2$.

4. Ricerca degli zeri della funzione, ovvero soluzione dell'equazione f(x) = 0. La frazione è uguale a 0 se e solo se lo è il numeratore, dunque l'equazione si riduce a $x + 1 = 0$ e quindi $x = -1$ Vi è dunque un solo zero per $x = -1$
5. Studio del segno della funzione, ovvero soluzione della disequazione f(x) > 0. Qui occorre considerare anche il segno del denominatore e considerare il segno dei tre fattori (x + 1), (x - 2), (x + 2) e riassumere con il solito schema

                           -2      -1          +2
   x + 2 > 0    ------------o+++++++++++++++++++++++++++++++++
   x + 1 > 0    --------------------o+++++++++++++++++++++++++
   x - 2 > 0    --------------------------------o+++++++++++++
                     -         +          -            +       
   

   La funzione è positiva per (-2 < x < -1) V (x > +2).
6. Ricerca di eventuali massimi e minimi. La derivata della funzione può calcolarsi con la regola della derivata del quoziente:

   $ y' = \frac{x^2 - 4 - (x + 1)2x}{(x^2 - 4)^2} = \frac{x^2 - 4 - 2x^2 - 2x}{(x^2 - 4)^2} = \frac{-x^2 - 2x - 4}{(x^2 - 4)^2} < 0 $

   Il numeratore è l'opposto di un falso quadrato dunque è sempre negativo; il denominatore è un quadrato e quindi sempre positivo; e quindi la derivata è sempre negativa, e la funzione è decrescente per ogni valore di $x$ nel dominio.