Grafico della funzione

        x3
y = -----------
     2(x - 1)2

2y(x − 1)2 = x3

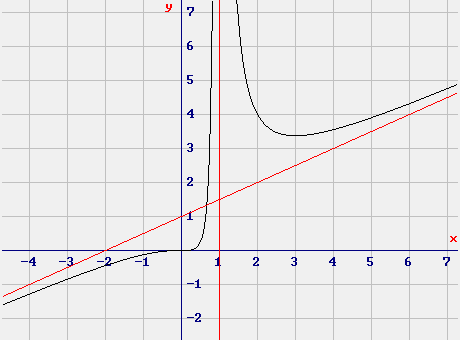
1. Insieme di definizione è R − {1} dovendo essere il denominatore x − 1 ≠ 0 e quindi x ≠ 1.
2. Ricerca di eventuali asintoti verticali per x = 1 ci può essere un asintoto verticale; verifichiamolo calcolando i due limiti:
   

            x3           (1 + dx)3           1 + 3.dx + 3.dx2 + dx3 
    lim -------- = st(--------------) = st(-------------------------) = +∞
   x→1+  (x − 1)2      (1 + dx − 1)2              dx2
   
            x3           (1 - dx)3           1 - 3.dx + 3.dx2 - dx3 
    lim -------- = st(--------------) = st(-------------------------) = +∞
   x→1-  (x − 1)2      (1 - dx − 1)2              dx2
   
   

   dunque vi è un asintoto verticale doppio.
3. Ricerca di eventuali asintoti obliqui. Il polinomio al numeratore ha grado superiore a quello del denominatore, dunque può esserci un asintoto obliquo, come si verifica con i limiti:

            f(x)             x3              1/dx3                   1/dx3                 1            1
   m = lim ------ = lim (----------) = st(---------------) = st(---------------) = st(------------) = ---
      x→+∞   x      x→+∞  2x(x - 1)2       2/dx(1/dx - 1)2         2(1 - dx)2/dx3       2(1 - dx)2      2
   
                               x3        x         x3 - x(x2 - 2x + 1)         2x2 - x
   q = lim f(x) - mx = lim ---------- - --- = lim -------------------- = lim --------- = 1
      x→+∞            x→+∞  2(x - 1)2    2    x→+∞    2(x - 1)2           x→+∞  2(x - 1)2 
   
   
   
   

   I due limiti si possono calcolare in modo ancor più semplice con la regola de l'Hopital. La cubica ha comunque un asintoto obliquo y = x/2 + 1.
4. Ricerca degli zeri della funzione, ovvero soluzione dell'equazione f(x) = 0. La frazione è uguale a 0 se e solo se lo è il numeratore, dunque l'equazione si riduce a

      x3 = 0   e quindi  x = 0
   

   Vi è dunque un solo zero nell'origine.
5. Studio del segno della funzione, ovvero soluzione della disequazione f(x) > 0. Qui occorre considerare anche il segno del denominatore e considerare il segno dei tre fattori (x + 1), (x - 2), (x + 2) e riassumere con il solito schema

                               0      +1
    x3 > 0       --------------o++++++++++++++++++++++++
   (x - 1) > 0   ++++++++++++++++++++++o++++++++++++++++
                        -          +             +       
   

   La funzione è positiva per (x > 0)
6. Ricerca dei massimi, dei minimi e dei flessi. Calcoliamo la derivata:

         3x2(x - 1)2 - x3.2(x - 1)    3x2(x - 1) - 2x3      3x3 - 3x2 - 2x3      x3 - 3x2
   y' = -------------------------- = ----------------- = ----------------- = ----------
               4(x - 1)4                 4(x - 1)3              4(x - 1)3      4(x - 1)3
   

   La derivata si annulla quando si annulla il numeratore x³ - 3x² = x²(x - 3) = 0. Le soluzioni sono due: x = 0, x = 3. Nello studio del segno va considerato anche il denominatore (x - 1)³:

                              0    +1     +3
    x2 > 0      ++++++++++++++o++++++++++++++++++++++++
   x - 3 > 0    --------------------------o++++++++++++
   (x - 1)3 > 0  -------------------o++++++++++++++++++
                     + /       + /    - \       +  /     
   

   Ne segue che:
   • Per x = 0 c'è un flesso a tangente orizzontale.
   • Per x = 1 c'è l'asintoto verticale doppio già visto.
   • Per x = 3 c'è un minimo: Min(3; 27/8).