

|
Come si è visto la legge dell'interesse composto è tanto più vantaggiosa per l'investitore quando maggiore è il numero di cedole pagate in un periodo. Ma quanto vantaggiosa? C'è un limite superiore al vantaggio? Per quantificare prendiamo il caso più semplice, quello nel quale l'interesse deve essere del $100\% = 1$ dopo un periodo; in tal casa ovviamente dopo un periodo il capitale raddoppia: $$ C = C_0 \left( 1 + 1 \right)^1 = 2$$Se si distribuisce questo interesse $1$ su $n$ cedole, ogni cedola varrà $t = \frac{1}{n}$ e quindi la legge diventa: $$ C = C_0 \left( 1 + \frac{1}{n} \right)^n$$ o anche dividendo per $C_0$: $$ \frac{C}{C_0} = \left( 1 + \frac{1}{n} \right)^n$$ che mette in evidenza il fattore di crescita; a lato una tabella calcola i valori di questo fattore per diversi valori di $n$. Appare evidente che il fattore cresce sempre più lentamente assestandosi su un valore poco superiore a $2,7$. Si può dimostrare che tale fattore è strettamente crescente e non può superare il numero $3$ e quindi la sequenza è limitata. Interpretata come un numero iperreale che chiameremo $\eta$ possiamo definirlo così: $$ \eta = \left( 1 + \frac{1}{\omega} \right)^{\omega} = \left( 1 + \epsilon \right)^{\omega}$$ Dove $\omega$ è il numero infinitamente grande; essendo limitato questo numero iperreale ha una parte standard, che chiameremo $e$: $$ e = st\left(\left( 1 + \epsilon \right)^{\omega}\right)$$ o anche $$ e \simeq \left( 1 + \epsilon \right)^{\omega}$$ Il numero $e$, o di Nepero, le cui prime cifre sono $2,7182818 ...$, è uno dei numeri più importanti della matematica; ha nell'analisi un'importanza paragonabile a quella di $\pi$ in geometria. L'importanza del numero $e$ sta soprattutto in quella della funzione esponenziale che ha per definizione base $e$; la funzione si scrive $y=e^x$ o anche $y=exp(x)$. Eulero approssima il numero $e$
Eulero trovò un altro metodo, molto più efficiente per approssimare $e$, sempre partendo dalla definizione $e \simeq (1+\epsilon)^\omega$. Applicando a questa potenza ad esponente infinitamente grande il binomio di Newton, Eulero ottiene successivamente: $(1+ε)^ω = 1 + \binom{ω}{1}ε + \binom{ω}{2}ε^2 + \binom{ω}{3}ε^3 ... \\ = 1 + \frac{ω}{1}ε + \frac{ω(ω-1)}{2!}ε^2 + \frac{ω(ω-1)(ω-2)}{3!}ε^3 ... \\ = 1 + 1 + \frac{ω^2-ω}{2!}ε^2 + \frac{ω^3-3ω^2+2ω}{3!}ε^3 ... \\ = 1 + 1 + \frac{1-ε}{2!} + \frac{1-3ε+2ε^2}{3!} ... \\ \simeq 1 + 1 + \frac{1}{2!} + \frac{1}{3!} ... $ Quindi il numero $e$ viene ad essere la somma transfinita, dei reciproci dei fattoriali. Bastano arrivare al termine $\frac{1}{14!}$ per avere 10 cifre decimali esatte: $2,7182818285...$, una precisione che con il primo metodo richiede milioni di iterazioni.
|
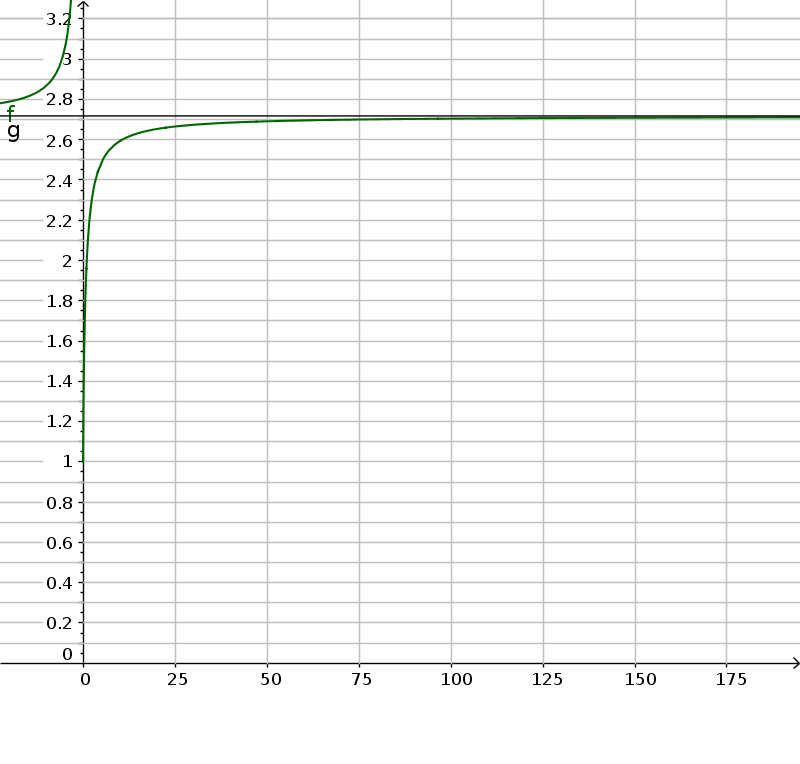 Andamento grafico di $\left( 1 + \frac{1}{x} \right)^x$
Andamento grafico di $\left( 1 + \frac{1}{x} \right)^x$
|