

|
La legge dell'interesse composto differisce da quella dell'interesse semplice perché si ammette che la cedola non venga staccata dal capitale ma venga versata direttamente nel capitale, andandolo ad aumentare; la cedola successiva dovrà quindi essere calcolata non sul capitale iniziale $C_0$ ma sul capitale aggiornato; quindi per esempio a un tasso di interesse del $5\%$ composto, con un capitale iniziale di $10 €$, la prima cedola calcolata su $10 €$ sarà di 0,5 € come per l'interesse semplice, ma i 50 cent. vanno subito a incrementare il capitale a $10,50 €$; calcolato in altro modo è $C = 10 (1+0,05) = 10*1,05 = 10,50 €$ quindi ad ogni cedola il capitale si moltiplica per $1,05$. La seconda cedola quindi sarà calcolata con il 5% di 10,50, quindi $10,50 \times 1,05 = 10 \times 1,05 \times 1,05= 11,025 €$; la terza cedola comporterà un'ulteriore moltiplicazione per il fattore $1,05$ e così via. In definitiva il capitale si calcola con una moltiplicazione ripetuta, e cioé con una potenza. La legge dell'interesse composto si scrive quindi così: $$ C = C_0 \left( 1 + t \right)^n \quad n \in \mathbb{N}$$Si tratta di una funzione che ha la variabile indipendente $n$ all'esponente, quindi una funzione esponenziale di variabile intera con dominio $\mathbb{N}$. Anche questa funzione si può estendere ai numeri reali, in due modi; considerando il numero di periodi come un numero reale si ha la funzione: $$ C = C_0 \left( 1 + t \right)^x \quad x \in \mathbb{R}$$ che è una funzione esponenziale nel senso classico del termine. Anche qui equivale a che l'interesse sia pagato in modo continuo, in pratica un interesse infinitesimo in corrispondenza ad un tempo infinitesimo. Volendo una formulazione più realistica basta usare la funzione a scalini, per esempio la floor: $$ C = C_0 \left( 1 + t \right)^{\lfloor{x}\rfloor} $$ In questo modo il capitale aumenta a scatti alla scadenza di ogni periodo quando viene pagata la cedola. A destra il grafico delle due funzioni; nel caso continuo si tratta di una curva esponenziale. Sono di questo tipo per esempio: 1) gli interessi bancari; la banca alla scadenza della cedola, versa l'importo dovuto direttamente sul conto corrente del cliente; di solito il periodo è trimestrale, ma può essere diverso a seconda del contratto; 2) i fondi di investimento nei quali gli interessi maturati si accumulano nel capitale investito; ma in questo caso gli interessi non sono fissi e quindi l'andamento della funzione è imprevedibile a priori. Con la legge dell'interesse composto c'è una differenza significativa a seconda del periodo del pagamento della cedola; così se il tasso annuo è $t = 5\%$, pagato in una sola cedola annuale dà ogni anno il $5\%$, pagato in due cedole semestreli del $2,5\%$ dà per ogni anno il $5,0625\% (1,025^2 = 1,050625)$; in quattro cedole dell'$1,25\%$ dà annualmente il $5,0945337\% (1,0125^4 = 1,050945337)$; insomma più frequenti sono le cedole maggiore è il vantaggio per l'investitore che però sembra crescere via via più lentamente. |
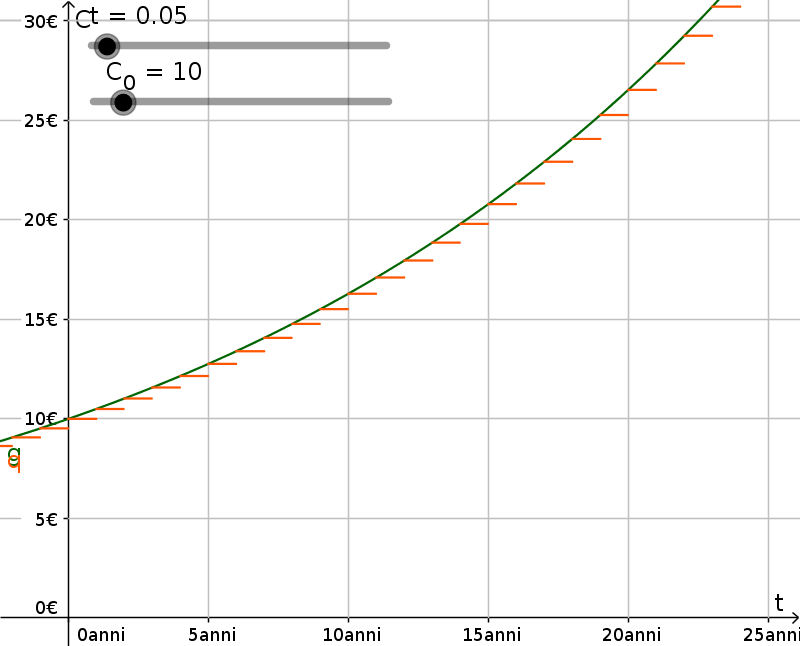 Interesse composto, andamento
Interesse composto, andamento
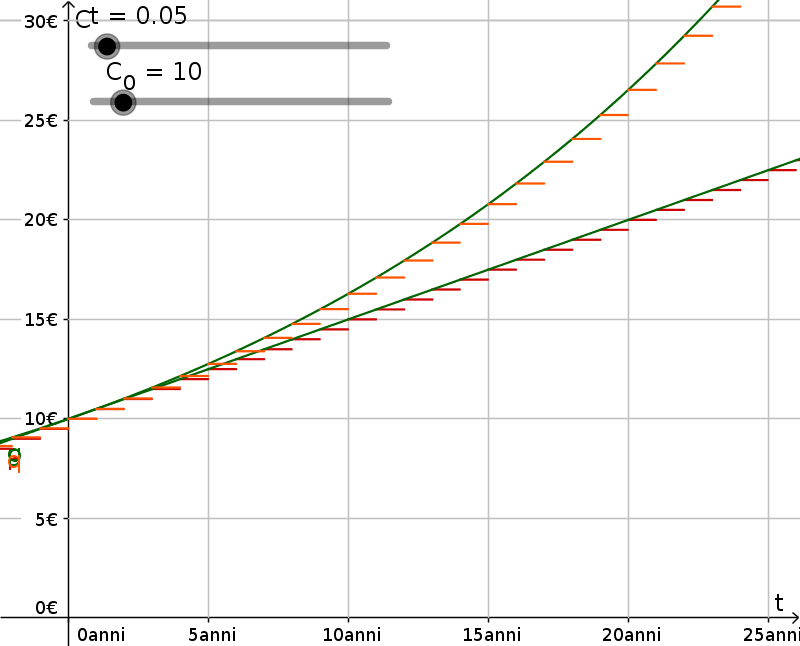 Confronto tra interesse composto (sopra) e interesse semplice (sotto)
Confronto tra interesse composto (sopra) e interesse semplice (sotto)
|
Calcolare la derivata delle seguenti funzioni