Studio di funzione irrazionale

Studio della funzione irrazionale √(4 − x²)

Studiare la funzione

    
y = √(4 − x²)

si tratta di una funzione algebrica irrazionale.

Insieme di definizione L'argomento della radice quadrata deve essere positivo o nullo, in altre parole deve essere
```
4 − x² ≥ 0
```
Risolvendo la disequazione, si ha (2 − x)(2 + x) ≥ 0 e quindi:
```
                 -2        +2
2 - x  +++++++++++++++++++++o---------------
2 + x  -----------o+++++++++++++++++++++++++
             −         +           −
```
Dunque la funzione è definita per −2 ≤ x ≤ +2.
Il dominio è l'intervallo [−2, +2]
Ricerca di eventuali asintoti verticali per x = ±2 la funzione vale zero e quindi non ci sono asintoti verticali.
Ricerca di eventuali asintoti obliqui: non possono esserci asintoti orizzontali od obliqui, perché non ha senso calcolare i limiti all'infinito per una funzione limitata all'intervallo finito [−2, +2]
Zeri della funzione: si tratta di risolvere l'equazione 4 − x² = 0 già risolta per l'insieme di definizione. Gli zeri sono x = −2 e x = +2
Studio del segno della funzione: il radicale è sempre positivo salvo per x = ± 2 dove si annulla.
Ricerca di massimi, minimi e flessi: calcoliamo la derivata della funzione secondo la regola della funzione composta:
```
y = √(t)
t = 4  − x²

dy/dt = 1/2√(t)
dt/dx = − 2x
```
La derivata è quindi:
```
              1            x
y' = − 2x ------------ = − ----------
         2√(x² − 4)     √(x² − 4)
```
La derivata, essendo il denominatore sempre positivo, ha il segno di −x, nagativa nel I quadrante, positiva nel II quadrante. La funzione è quindi decrescente nel I quadrante, crescente nel II.
La derivata si annulla per x = 0 e quindi riassumendo:
```
                   0
 - x  +++++++++++++o---------------
             +           −
             /            \
```
Per x = 0 c'è dunque un massimo Max(0;2).
Infine si noti che per x = ±2 la derivata vale 2/0, in altre parole tende a infinito per x →±2. Geometricamente questo significa che per x = ± 2 la funzione ha tangente verticale.
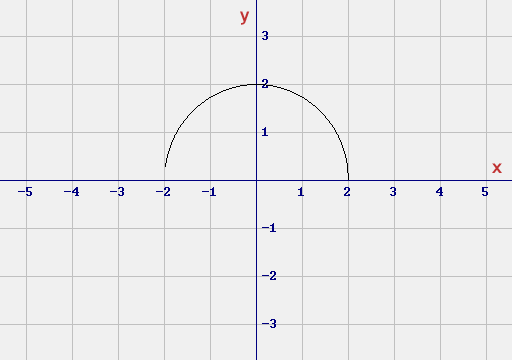
In definitiva si ottiene il grafico sopra riportato.
Osservazione N.1 Elevando al quadrato la funzione si ottiene:
```
y² = 4 − x²
```
o anche
```
x² + y² = 4
```
che altro non è che l'equazione di una circonferenza di raggio r = 2. La funzione studiata non è altro che la semicirconferenza al di sopra dell'asse delle x.
Osservazione N.2 Sostituendo nella funzione x con 2.cos(t) si ha:
```
y = √(4 − 4.cos²(t)) = 2.√(1 − (cos²(t)))
```
e per l'identità goniometrica fondamentale:
```
y = 2.√(sin²(t)) = 2.sin(t)
```
Se ne ricavano le cosiddette equazioni parametriche della circonferenza, analoghe a quelle dell'iperbole equilatera.
```
x = 2.cos(t)
y = 2.sin(t)
```