

Il primo e il terzo paradosso di Zenone hanno qualcosa in comune?
Sì! Il concetto di infinitamente piccolo!
Nel primo paradosso abbiamo visto che la sequenza dei segmenti mancanti ad Achille nel primo paradosso è espressa da questa sequenza di numeri razionali:
$$ \alpha = \left\langle 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16} ... \frac{1}{2^n} ... \right\rangle $$
Converremo di chiamare numero iperreale infinitamente piccolo il numero rappresentato da questa sequenza, un po' come i numeri reali sono rappresentati da sequenze di infinite cifre decimali. I numeri reali li ritroviamo anche tra gli iperreali come iperreali stabili: per esempio:
$$ 0 = \left\langle 0, 0, 0 ... 0... \right\rangle $$ $$ 1 = \left\langle 1, 1, 1 ... 1... \right\rangle $$ $$ N = \left\langle N, N, N ... N... \right\rangle $$
Il terzo paradosso, quello della freccia, ci porta invece in modo diverso al concetto di infinitamente piccolo; Leibniz introduce numeri infinitesimi rappresentati da simboli come $dx, dy$(*) come numeri che soddisfano queste condizioni:
| Un numero si dice infinitesimo o infinitamente piccolo, se ... $$ \forall{N} : 0 < {dx} < \frac{1}{N} $$ |
|
Ai numeri infinitesimi si applicano le normali proprietà dell'algebra: associativa, commutativa, distributiva ... |
Questa seconda proprietà, che Leibniz non dimostrò, rientra nel cosiddetto principio di estensione (in inglese di transfer), la cui trattazione dettagliata esula dagli obiettivi di questo corso.
Che relazione c'è tra i numeri infinitesimi definiti in questo modo, e quel numero $\alpha$ infinitamente piccolo che emerge dal primo paradosso?
Mostriamo che il numero $\alpha$ soddisfa la prima condizione; innanzitutto che il numero $\alpha$ è sempre maggiore di zero, infatti confrontando i due numeri:
$$ \begin{matrix} \alpha = \quad & 1 & \frac{1}{2} & \frac{1}{4} & \frac{1}{8} & \frac{1}{16}& ... \\ 0 = \quad & 0 & 0 & 0 & 0 & 0 & ... \end{matrix} $$
Appare evidente che ogni elemento di $\alpha$ è maggiore di zero, quindi è, definitivamente, all'unanimità, $\alpha > 0$.
Mostriamo ora che il numero $\alpha$ è minore di qualsiasi numero reale piccolo quanto si vuole$\frac{1}{N}$; cominciamo ad esempio con il numero $\frac{1}{64}$ e mostriamo che $\alpha < \frac{1}{64}$
$$ \begin{matrix} \frac{1}{64} = \quad & \frac{1}{64} & \frac{1}{64} & \frac{1}{64} & \frac{1}{64} & ... & \frac{1}{64} & \frac{1}{64} & ... \\ \alpha = \quad & 1 & \frac{1}{2} & \frac{1}{4} & \frac{1}{8} & ... & \frac{1}{64} & \frac{1}{128} & ... \end{matrix} $$
Qui il numero $\alpha$ è inizialmente maggiore di $\frac{1}{64}$ ma prima o poi si arriva ad avere un termine (qui $\frac{1}{128}$) che è minore del corrispondente elemento di $\frac{1}{64}$ e questo vale per tutti i numeri successivi che sono infiniti e quindi ovviamente sono la maggioranza assoluta. Quindi è, definitivamente, a maggioranza infinita, $\alpha < \frac{1}{64}$
Generalizzando questo esempio possiamo dimostrare che il numero $\alpha$ è minore di qualsiasi numero reale piccolo quanto si vuole$\frac{1}{N}$:
$$ \begin{matrix} \frac{1}{N} = \quad & \frac{1}{N} & \frac{1}{N} & \frac{1}{N} & \frac{1}{N} & ... & \frac{1}{N} & ... \\ \alpha = \quad & 1 & \frac{1}{2} & \frac{1}{4} & \frac{1}{8} & ... & \frac{1}{M} & ... \end{matrix} $$
Anche qui il numero $\alpha$ è inizialmente maggiore di $\frac{1}{N}$ ma prima o poi si arriva ad avere un termine con denominatore maggiore di $N$ e quindi minore di $\frac{1}{N}$ e questo vale per tutti i numeri successivi che sono infiniti e quindi ovviamente sono la maggioranza assoluta. Quindi è, definitivamente, a maggioranza infinita, $\alpha < \frac{1}{N}$
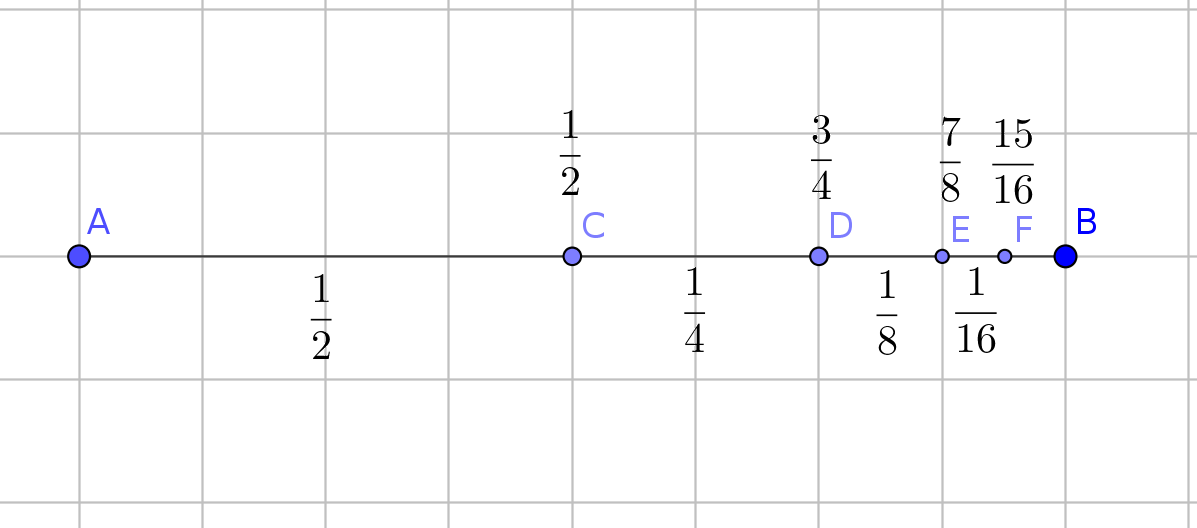
Ai numeri iperreali si possono poi estendere le operazioni aritmetiche, addizione, sottrazione, moltiplicazione, divisione, potenza, radicale semplicemente eseguendo l'operazione termine a termine. Per esempio (vedi primo paradosso) la sottrazione $1-\alpha$:
$$ \begin{matrix} 1 = \quad & 1 & 1 & 1 & 1 & ... & 1 \\ \alpha = \quad & 1 & \frac{1}{2} & \frac{1}{4} & \frac{1}{8} & ... & \frac{1}{2^N} & ... \\ 1 -\alpha = \quad & 0 & \frac{1}{2} & \frac{3}{4} & \frac{7}{8} & ... & 1-\frac{1}{2^N} & ... \end{matrix} $$
Ne segue che restano valide le proprietà associativa, commutativa, distributiva ... e quindi un numero iperreale come $\alpha$ equivale in tutto per tutto a un infinitesimo di Leibniz.