Zenone sbaglia a ragionare quando sostiene che la freccia scagliata è immobile.
Il terzo è quello, appena menzionato, della freccia che, se pur scagliata sta ferma. Ma una siffatta conclusione dipende dall'assunzione che il tempo sia costituito da istanti: se non si concede questo il ragionamento non tiene. [Aristotele, Fisica VI.9]
Nel terzo paradosso Zenone immagina una freccia, simbolo della velocità: in ogni istante (tempo di durata nulla) la freccia è immobile (spostamento nullo), dunque il movimento della freccia risulta da una successione di stati nei quali la freccia ha spostamento nullo e quindi è immobile. Aristotele confuta il ragionamento di Zenone negando l'esistenza degli istanti, intesi come tempi indivisibili; i Greci non avevano il concetto di zero, oggi diremmo che tempo indivisibile equivale a intervallo di tempo nullo $\Delta {t} = 0$.
Oggi ben più della freccia l'oggetto familiare più veloce è l'aereo; la foto accanto riprende un aereo in atterraggio, velocità intorno ai 200 km/h ovvero 60 m/s. L'aereo appare immobile, sospeso a mezz'aria, sopra la pista, pure è in movimento a velocità molto elevata; basta una foto come questa per esemplificare il paradosso.
Come è possibile che l'aereo appaia immobile, mentre è ancora molto veloce? Il fotografo risponderà che il tempo di esposizione era di 1/640 sec, tempo impercettibile per il cervello umano; in un tempo così breve a quella velocità l'aereo si è spostato di circa 9 cm, che sul fotogramma può equivalere a un pixel o poco più, impercettibile all'occhio umano che osserva la fotografia.
La parola chiave è impercettibile, inferiore a qualsiasi tempo percettibile: l'aereo appare fermo perché lo spostamento nel tempo impiegato per fare la foto, è impercettibile all'occhio umano, minore di quel che l'occhio è in grado di discernere.
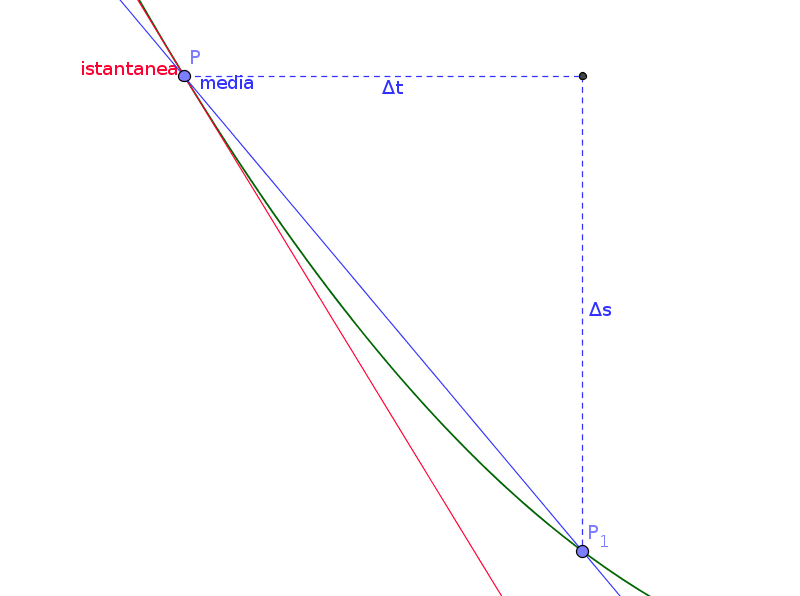Ma esaminiamo il paradosso usando le notazioni della fisica e della matematica moderne; la velocità media $v$ di un corpo che si sposta da $A$ a $B$ è per definizione il rapporto tra lo spazio percorso $\Delta{s}$ e il tempo impiegato a percorrerlo $\Delta{t}$:
$$ v = \frac{\Delta{s}}{\Delta{t}} $$
Ma se il tempo si riduce ad un istante di durata nulla, anche lo spazio percorso è nullo e la velocità istantanea si riduce a:
$$ v = \frac{0}{0} $$
che come ogni studente sa è un'indeterminata. Zenone invece, non avendo la definizione moderna di velocità, concludeva erroneamente che spostamento nullo equivale a velocità nulla. Il paradosso cambia natura, ma in peggio! Zero diviso zero vorrebbe dire un numero che moltiplicato per zero fa zero, ovverosia qualsiasi numero! Risultato indeterminato appunto.
Il problema è equivalente a quello matematico della ricerca della tangente a una curva.
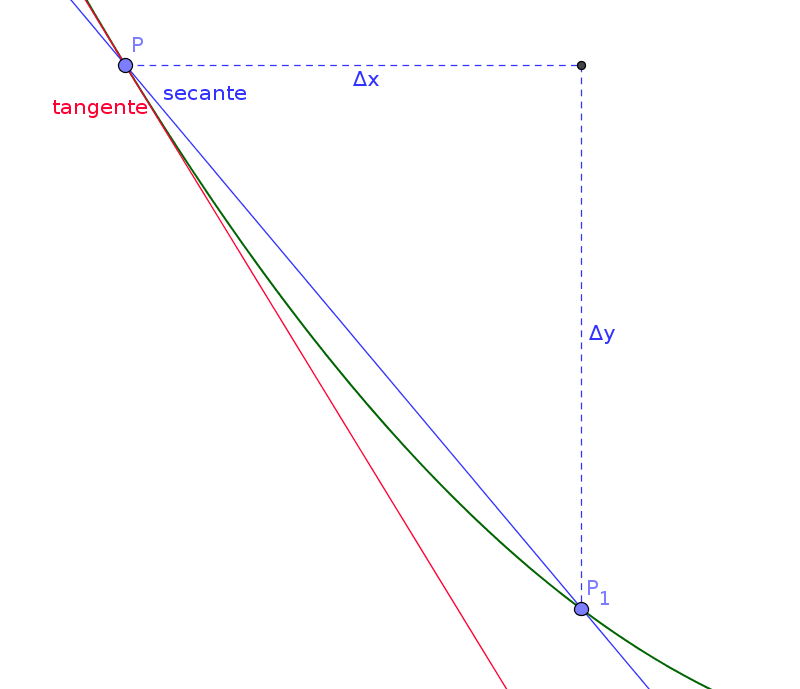
Duemila anni dopo Zenone, Leibniz e Newton propongono, con notazioni diverse ma basate sulla stessa idea di fondo, un modo di aggirare il paradosso che in qualche misura richiama le obiezioni di Aristotele. In sostanza l'idea è che istante di tempo non significhi tempo indivisibile, di durata nulla, ma tempo di durata infinitamente piccola o infinitesima e quindi divisibile; un numero che sia impercettibile quindi minore di ogni grandezza percettibile, ma diverso da zero.
Idealizzando la nozione di impercettibile si arriva a concepire un numero inferiore ad ogni numero reale ma pur sempre maggiore di zero, che chiameremo appunto numero infinitesimo o infinitamente piccolo.
Occorre quindi introdurre un nuovo tipo di numeri, numeri detti anche non-archimedei perché non rispettano il postulato di Eudosso-Archimede. Usando la notazione di Leibniz un numero infinitesimo positivo $dx$ è un numero maggiore di zero, quindi diverso da zero, ma al tempo stesso minore di un qualsiasi numero reale positivo. In simboli si può scrivere:
$$ \forall{N} \quad : \quad 0 < {dx} < \frac{1}{N} $$
dove $N$ è un qualsiasi numero naturale.
Per Leibniz quindi la pendenza $m$ della tangente, ovvero la velocità istantanea $v$ è data da un quoziente di infinitesimi:
$$ m = \frac{dy}{dx} \quad ; \quad v = \frac{ds}{dt}$$
Può sembrare un inutile artificio questo di sostituire lo zero con un numero infinitamente piccolo, pure da questo artificio nasce un nuovo calcolo, il calcolo infinitesimale. Per maggiori dettagli vedi la pagina La derivata alla maniera di Leibniz