

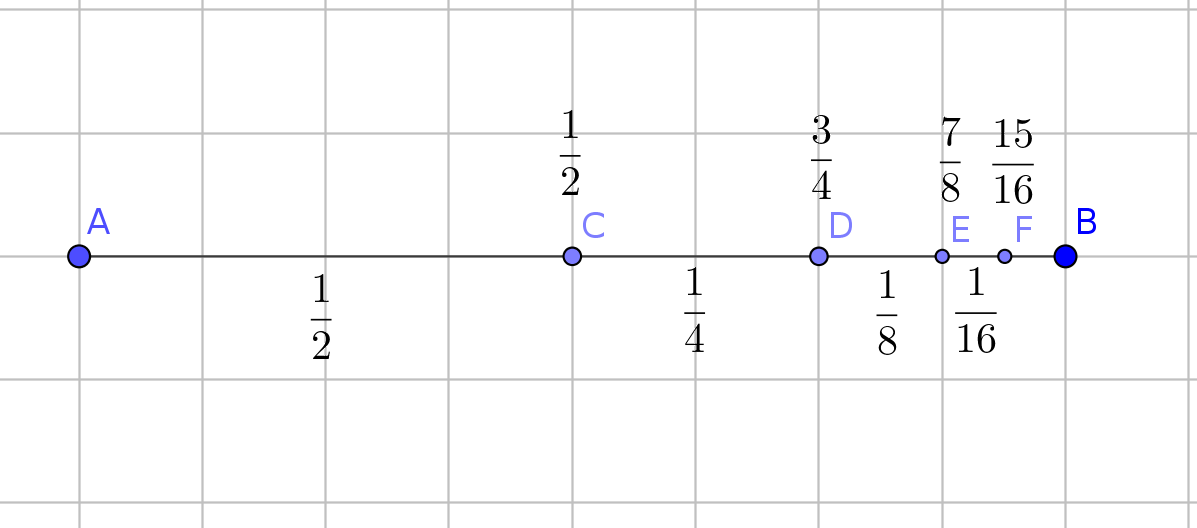
Il primo paradosso è quello del segmento: dato un segmento $AB$ neanche il pie' veloce Achille(*) potrà mai percorrerlo tutto; infatti dovrà prima raggiungere il punto $C$ medio tra $A$ e $B$, poi il punto $D$ medio tra $C$ e $B$, e così via all'infinito. Quindi Achille non raggiungerà mai il punto $B$.
Non intendo qui discutere le possibili soluzioni del paradosso, basta ricordare che la più semplice e realistica è quella atomica o quantistica, che cioè non sia possibile continuare la suddivisione all'infinito, prima o poi si arriverà a segmenti indivisibili.
Riscriviamo invece questo famoso paradosso usando le notazioni moderne; per prima cosa scriviamo in frazioni, posta uguale ad 1 la distanza $AB$ la strada mancante a $B$ è successivamente:
$$ 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16} ... \frac{1}{2^n} ... $$
La distanza da B diventa sempre più piccola, potremmo dire che alla fine della corsa, se di fine della corsa si può parlare, sarà infinitamente piccola.
Scriviamo ora le successive distanze del punto $B$ da $A$:
$$ 1, 1, 1, 1, 1 ... 1 ... $$
Può sembrare banale, ma serve a ricordarci che il punto $B$ è fisso, non si muove a differenza di quanto accade nel secondo paradosso dove è sostituito da una tartaruga che seppur lentamente si muove.
Scriviamo ora le successive distanze percorse da Achille, che sono poi le differenze tra i numeri della seconda serie e della prima:
$$ 0, \frac{1}{2}, \frac{3}{4}, \frac{7}{8}, \frac{15}{16} ... \frac{2^n -1}{2^n} ... $$
La distanza percorsa è sempre più vicina ad uno; la diremo infinitamente vicina ad 1.
Questo paradosso, scritto in questo modo, suggerisce l'idea di introdurre un nuovo tipo di numeri, rappresentati da sequenze di infiniti numeri reali; questi numeri si chiamano numeri iperreali. Possiamo chiamare il primo numero (distanza successive di Achille da $B$) con la lettera greca $\alpha$ così:
$$ \alpha = \left\langle 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16} ... \frac{1}{2^n} ... \right\rangle $$
Un siffatto numero di dice numero infinitamente piccolo o infinitesimo ed ha le stesse proprietà che molti secoli dopo Zenone, Leibniz attribuisce ai suoi infinitesimi e cioè quella di essere al tempo stesso maggiori di zero e minori di ogni numero reale per quanto piccolo. La verifica si trova alla pagina numeri infinitesimi o infinitamente piccoli.
La seconda sequenza è la rappresentazione di un numero iperreale stabile che equivale al numero $1$:
$$ 1 = \left\langle 1, 1, 1, 1, 1 ... 1 ... \right\rangle $$
E quindi la terza sequenza, strada percorsa da Achille, equivale a una differenza di iperreali, il numero $\beta = 1-\alpha$
$$ \beta = 1 - \alpha = \left\langle 0, \frac{1}{2}, \frac{3}{4}, \frac{7}{8}, \frac{15}{16} ... \frac{2^n -1}{2^n} ... \right\rangle $$
Analogamente il numero 0 si rappresenta:
$$ 0 = \left\langle 0, 0, 0, 0, 0 ... 0 ... \right\rangle $$
In conclusione si può dire che $\alpha$ è infinitamente vicino a zero, $\beta$ infinitamente vicino a uno.
Il numero $\alpha$ è un infinitesimo nel senso di Leibniz.