Una funzione goniometrica y = sin(2x)

Studio della funzione y = sin(2x)

Studiare la funzione goniometrica
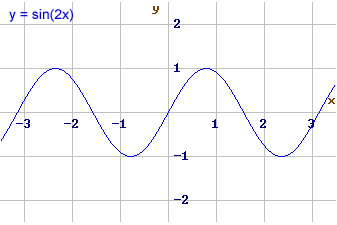
y = sin(2x)	Questa funzione non è altro che un sinusoide con periodo dimezzato. Viene chiamata la seconda armonica del seno.

Insieme di definizione il seno è definito per ogni valore di x, dunque I = R.
Periodo della funzione la funzione seno ha periodo 2π, sin(2x) ha periodo dimezzato π. Basterà quindi studiare la funzione in un intervallo di ampiezza π, p.es. [0;,+π[.
Simmetrie cambiando x in -x la funzione cambia di segno, si tratta quindi di una funzione dispari, con simmetria centrale rispetto all'origine.
Ricerca di eventuali asintoti il seno è una funzione limitata tra -1 e +1, anche la somma di due funzioni sinusoidali sarà limitata; dunque non esistono asintoti.
Ricerca degli zeri della funzione, ovvero soluzione dell'equazione sin(2x) = 0. Si tratta di un'equazione goniometrica elementare nell'incognita 2x.
```
    sin(2x) = 0    ==>    2x = 0 + kπ
```
e dividendo tutto per 2:
```
               π
    x = 0 + k.---
               2
```
Limitando lo studio all'intervallo [0, + π] si hanno due zeri x= 0 e x = π/2 = 1.57...
Calcolo delle derivate. La derivata di sin(x) è cos(x). La funzione sin(2x) è una funzione composta, e la sua derivata vale:
```
	y = sin(t)    y' = cos(t)
	t = 2x        t' = 2

	f'(x) = 2.cos(t) = 2.cos(2x)
```
Procedendo in modo analogo e ricordando la regola della derivata del coseno si calcola anche la derivata seconda:
```
        f"(x) = -4.sin(2x)
```
Ricerca dei massimi, dei minimi. Conviene usare il II metodo. L'equazione f'(x) = 0 diventa
```
   2.cos(2x) = 0
```
e dividendo tutto per 2:
```
   cos(2x) = 0
```
Abbiamo anche qui un'equazione goniometrica elementare in 2x
```
                       π
   2x = arccos(0) = ± --- + 2k.π
                       2
```
e dividendo tutto per 2:
```
         π
   x = ± --- + k.π
         4
```
I punti stazionari della curva sono quindi, nell'intervallo studiato [0, π[, due:
```
   x = π/4 = 0,7854...  [per k=0]
   x = 3.π/4 = 2,3562... [per k=1]
```
Per decidere se si tratta di massimi, minimi o flessi va calcolata la derivata seconda per ognuno:
```
   f"(π/4)   = -4.sin(π/2)   = -4.1 = -4 < 0 ==> c'è un massimo 
   f"(3.π/4) = -4.sin(3.π/2) = -4.(-1) = +4 > 0    ==> c'è un minimo
```
Le ordinate dei quattro punti si ottengono calcolando la funzione di partenza sin(x)+sin(2x) per ognuno dei quattro punti e in definitiva si trova:
```
   Max(π/4, 1)
   Min(3.π/4, -1)
```
Ricerca dei flessi: si tratta di uguagliare a zero la derivata seconda calcolata sopra:
```
-4.sin(2x) = 0
```
cosa che equivale a risolvere sin(2x) = 0; gli zeri della derivata seconda coincidono con gli zeri della funzione. Considerando poi la derivata terza:
```
f'''(x) = -8.cos(2x)
```
poichè per la prima identità goniometrica fondamentale cos(2x) vale ±1 se sin(2x) = 0, ne segue che la derivata seconda è alternativamente -8 e +8; dunque tutti gli zeri della funzione sono anche punti di flesso.

Riassumendo tutti questi risultati si ottiene il grafico riportato sopra.